
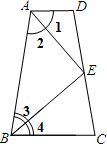
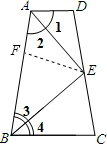
 如图,凸四边形ABCD中,点E在边CD上,连接AE、BE.给出下列五个关系式:①AD∥BC;②DE=EC;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为已知条件、另外两个关系式作为结论,可以构成一些命题(下面各小题的命题须符合此要求).
如图,凸四边形ABCD中,点E在边CD上,连接AE、BE.给出下列五个关系式:①AD∥BC;②DE=EC;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为已知条件、另外两个关系式作为结论,可以构成一些命题(下面各小题的命题须符合此要求).| 序号 | 条件 | 结论 | 命题真假 | |||
| 1 | ③∠1=∠2 | ④∠3=∠4 | ⑤AD+BC=AB | ①AD∥BC | ②DE=EC | 真 |
| 2 | ②DE=EC | ④∠3=∠4 | ⑤AD+BC=AB | ①AD∥BC | ③∠1=∠2 | 真 |
| 3 | ②DE=EC | ③∠1=∠2 | ⑤AD+BC=AB | ①AD∥BC | ④∠3=∠4 | 真 |
| 4 | ②DE=EC | ③∠1=∠2 | ④∠3=∠4 | ①AD∥BC | ⑤AD+BC=AB | 假 |
| 5 | ①AD∥BC | ④∠3=∠4 | ⑤AD+BC=AB | ②DE=EC | ③∠1=∠2 | 真 |
| 6 | ①AD∥BC | ③∠1=∠2 | ⑤AD+BC=AB | ②DE=EC | ④∠3=∠4 | 真 |
| 7 | ①AD∥BC | ③∠1=∠2 | ④∠3=∠4 | ②DE=EC | ⑤AD+BC=AB | 真 |
| 8 | ①AD∥BC | ②DE=EC | ⑤AD+BC=AB | ③∠1=∠2 | ④∠3=∠4 | 真 |
| 9 | ①AD∥BC | ②DE=EC | ④∠3=∠4 | ③∠1=∠2 | ⑤AD+BC=AB | 真 |
| 10 | ①AD∥BC | ②DE=EC | ③∠1=∠2 | ④∠3=∠4 | ⑤AD+BC=AB | 真 |
 ,
, ,
,

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
 已知凸四边形ABCD的对角线AC,BD相交于点O,且△ABC,△ACD,△ABD的面积分别为S1=5,S2=10,S3=6.求△ABO的面积(如图).
已知凸四边形ABCD的对角线AC,BD相交于点O,且△ABC,△ACD,△ABD的面积分别为S1=5,S2=10,S3=6.求△ABO的面积(如图).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD=
A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,凸四边形ABCD的四边AB、BC、CD、和DA的长分别是3,4,12,和13,∠ABC=90°,则四边形
如图,凸四边形ABCD的四边AB、BC、CD、和DA的长分别是3,4,12,和13,∠ABC=90°,则四边形查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com