解:(1)过C点向x轴作垂线,垂足为D,由位似图形性质可知△ABO∽△ACD,
∴
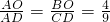
.
由已知A(-4,0),B(0,4)可知
AO=4,BO=4.
∴AD=CD=9,
∴C点坐标为(5,9),
设直线BC的解析式为y=kx+b,
∵A(-4,0),B(0,4)在一次函数解析式上,那么
-4k+b=0,b=4,
解得k=1,
化简得y=x+4;
(2)设抛物线解析式为y=ax
2+bx+c(a>0),由题意得
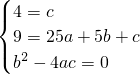
,
解得
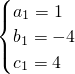
,
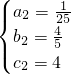
,
∴解得抛物线解析式为y
1=x
2-4x+4或y
2=

x
2+

x+4,
又∵y
2=

x
2+

x+4的顶点在x轴负半轴上,不合题意,故舍去.
∴满足条件的抛物线解析式为y=x
2-4x+4,
(准确画出函数y=x
2-4x+4图象)
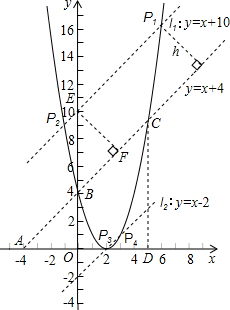
(3)将直线BC绕B点旋转与抛物线相交于另一点P,设P到直线AB的距离为h,
故P点应在与直线AB平行,且相距

的上下两条平行直线l
1和l
2上.
由平行线的性质可得
两条平行直线与y轴的交点到直线BC的距离也为

.
如图,设l
1与y轴交于E点,过E作EF⊥BC于F点,
在Rt△BEF中EF=h=

,∠EBF=∠ABO=45°,
∴BE=6.
∴可以求得直线l
1与y轴交点坐标为(0,10),
同理可求得直线l
2与y轴交点坐标为(0,-2),
∴两直线解析式l
1:y=x+10;l
2:y=x-2.
根据题意列出方程组:
(1)

;(2)

,
解得

;

;

;

,
∴满足条件的点P有四个,
它们分别是P
1(6,16),P
2(-1,9),P
3(2,0),P
4(3,1).
分析:(1)利用相似及相似比,可得到C的坐标.把A,B代入一次函数解析式即可求得解析式的坐标.
(2)顶点落在x轴正半轴上说明此函数解析式与x轴有一个交点,那么△=0,再把B,C两点即可.
(3)到直线AB的距离为

的直线有两条,可求出这两条直线解析式,和二次函数解析式组成方程组,求得点P坐标.
点评:本题用到的知识点为:可把位似比转换为相似三角形的相似比;到一条直线的距离为定值的直线是平行于已知直线的两条直线;平行直线的k的值相等.

 向右侧放大,B点的对应点为C.
向右侧放大,B点的对应点为C. 的点P.
的点P.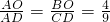 .
.
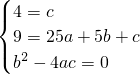 ,
,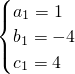 ,
, ,
, x2+
x2+ x+4,
x+4, x2+
x2+ x+4的顶点在x轴负半轴上,不合题意,故舍去.
x+4的顶点在x轴负半轴上,不合题意,故舍去. 的上下两条平行直线l1和l2上.
的上下两条平行直线l1和l2上. .
. ,∠EBF=∠ABO=45°,
,∠EBF=∠ABO=45°, ;(2)
;(2) ,
, ;
; ;
; ;
; ,
, 的直线有两条,可求出这两条直线解析式,和二次函数解析式组成方程组,求得点P坐标.
的直线有两条,可求出这两条直线解析式,和二次函数解析式组成方程组,求得点P坐标.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案 =2,∠ADC=30°
=2,∠ADC=30°