解:①设OB=x,则OA=2OB=2x;
Rt△OAB中,由勾股定理得:OA
2+OB
2=AB
2,
即x
2+4x
2=20,解得x=2;
∴OB=2,OA=4,同理可得OC=3;
故:A(0,4),B(-2,0),C(3,0),
∴

.
②∵D是AB的中点,
∴D(-1,2);
∵
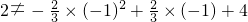
,
∴点D一在这条二次函数的图象上.
③∵

,
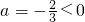
开口向下,
∴当

时,y随x的增大而减小.
分析:①根据∠ABC的正切值,可得到OA、OB的比例关系,用未知数表示出OA、OB的长,进而可在Rt△OAB中,利用勾股定理求出OA、OB的值,从而得到A、B的坐标;同理可在Rt△OAC中求出C点的坐标,进而可利用待定系数法求得该抛物线的解析式.
②根据A、B的坐标,易得D点的坐标,将其代入抛物线的解析式中进行验证即可.
③求二次函数的增减性,可从两方面考虑:1、抛物线的开口方向,2、抛物线的对称轴方程.
结合本题,将二次函数解析式化为顶点坐标式,即可得抛物线的对称轴方程,由于此抛物线的开口向下,因此在对称轴右侧的函数图象,y随x的增大而减小.
点评:此题主要考查了解直角三角形、二次函数解析式的确定、二次函数的增减性等知识,属于基础题,需要熟练掌握.

 如图所示,
如图所示,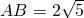 ,tan∠ABC=2,
,tan∠ABC=2,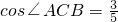 .
. .
.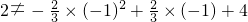 ,
, ,
,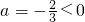 开口向下,
开口向下, 时,y随x的增大而减小.
时,y随x的增大而减小.
