已知以x为自变量的二次函数y=x2-(2m-2)x+(m2-m-2)的图象经过原点O,并与x轴相交于点M,且M在原点的右边.
(1)求这个二次函数的解析式;
(2)一次函数y=kx+b的图象经过点M,与这个二次函数的图象交于点N,且△OMN的面积等于3,求这个一次函数的解析式.
解:(1)∵二次函数y=x
2-(2m-2)x+(m
2-m-2)的图象经过原点O,
∴m
2-m-2=0,解得m=-1,m=2.
当m=-1时,二次函数的解析式为y=x
2+4x,它的图象经过原点,并与x轴相交于原点左边的点(-4,0),(不合题意,舍去);
当m=2时,二次函数的解析式为y=x
2-2x,它的图象经过原点,并与x轴相交于原点右边的点(2,0),符合题意,所以所求的二次函数的解析式为y=x
2-2x.
(2)由(1)中二次函数y=x
2-2x,它的图象经过原点,且与x轴相交于点M(2,0),
设点N的坐标为(x,y),则S
△OMN=

×2×|y|=3,
∴|y|=3,
∵二次函数y=x
2-2x的图形是开口向上,顶点为(1,-1)的抛物线;
∴抛物线上没有纵坐标为-3的点,
∴y=3,
当y=3时,x
2-2x=3,解得x=3,x=-1.
则点N
1(3,3),N
2(-1,3).
当函数y=kx+b的图形经过点M(2,0),N
1(3,3)时,则:
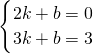
,
解得
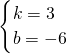
;
∴所求一次函数的解析式为y=3x-6.
当函数y=kx+b的图形经过点M(2,0),N
2(-1,3)时,则:
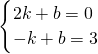
,
解得
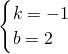
,
∴所求一次函数的解析式为y=-x+2.
分析:(1)已知函数图象经过原点,可将原点坐标代入抛物线的解析式中,可求得m的值,然后根据函数与x轴的另一交点在原点右边,可将不合题意的m的值舍去.
(2)可根据三角形OMN的面积求得N点的纵坐标的绝对值,然后将其代入抛物线的解析式中即可求得N点的坐标,根据M、N两点的坐标即可求出直线的解析式.
点评:本题主要考查了用待定系数法求二次函数的解析式及二次函数图象上点的坐标特点.

 ×2×|y|=3,
×2×|y|=3,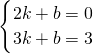 ,
,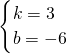 ;
;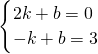 ,
,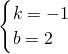 ,
,

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案