

分析 (1)四边形EFDG是平行四边形,理由为:如图1,连接AM,由E、F、G、H分别为中点,利用利用中位线定理得到两组对边相等,即可得证;
(2)四边形EFDG为正方形,理由为:如图2,连接CN,AM,分别交EF、CN于点L与K,由CB-BM求出CM的长,得到CM=BN,再由一对直角相等,AC=BC,利用SAS得到三角形ACM与三角形CBN全等,利用全等三角形对应边、对应角相等得到AM=CN,∠CAM=∠BCN,利用同角的余角相等,求出∠AKC为直角,利用两组对边平行的四边形为平行四边形得到四边形EFDG为平行四边形,再由一个内角为直角,且邻边相等即可得证.
解答 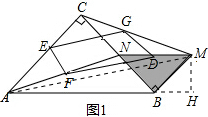 解:(1)四边形EFDG是平行四边形,
解:(1)四边形EFDG是平行四边形,
理由:如图1,连接AM,
∵E、F、D、G分别为AC、AN、MN、CM的中点,
∴FD=EG=$\frac{1}{2}$AM,EF=GD=$\frac{1}{2}$CN,
∴四边形EFDG是平行四边形;
(2)四边形EFDG是正方形,
理由:如图2,连接CN,AM,分别交EF、CN于点L与K,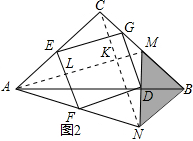 由已知得:点M和点D分别落在BC与AB边上,
由已知得:点M和点D分别落在BC与AB边上,
∴CM=CB-BM=4-2=2,
∴CM=BN,
∵∠ACM=∠CBN=90°,AC=BC,
∴△ACM≌△CBN(SAS),
∴AM=CN,∠CAM=∠BCN,
∵∠ACK+∠KCM=90°,
∴∠ACK+∠CAK=90°,
在△ACK中,∠AKC=180°-(∠ACK+∠CAK)=180°-90°=90°,
由(1)可得EG∥AM∥FD,EF∥CN∥GD,
∴四边形EFDG是平行四边形,
∴∠GEL=∠ELA=∠AKC=90°,
∴四边形EFDG是矩形,
∵EG=$\frac{1}{2}$AM=$\frac{1}{2}$CN=EF,
∴四边形EFDG是正方形.
点评 此题考查的是旋转的性质,涉及的知识有:平行四边形的判定与性质,正方形的判定,全等三角形的判定与性质,锐角三角函数定义,三角形中位线定理,熟练掌握判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  ∵$\widehat{AD}$=$\widehat{BC}$ ∴AB=CD | B. | 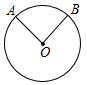 ∵$\widehat{AB}$的度数为40° ∴∠AOB=80° | ||
| C. | 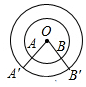 ∵∠AOB=∠A′OB′ ∴$\widehat{AB}$=$\widehat{A′B′}$ | D. | 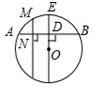 ∵MN垂直平分AD ∴$\widehat{MA}$=$\widehat{ME}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
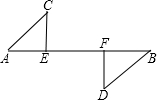 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com