
【题目】如图,已知抛物线y=ax2+![]() x+c经过A(4,0),B(1,0)两点,与y轴交于点C.
x+c经过A(4,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)在直线AC上方的抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
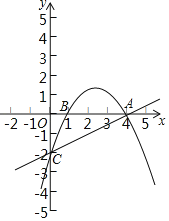
【答案】(1)![]() ;(2)存在,当D(2,1),△DAC面积的最大值为4.
;(2)存在,当D(2,1),△DAC面积的最大值为4.
【解析】
(1)由抛物线经过A(4,0),B(1,0),C(0,-2)三点,利用待定系数法即可求得该抛物线的解析式;
(2)设D点的横坐标为t(0<t<4),则D点的纵坐标为-![]() t2+
t2+![]() t-2,过D作y轴的平行线交AC于E.即可求得DE的长,继而可求得S△DCA=-(t-2)2+4,然后由二次函数的性质,即可求得点D的坐标及△DCA面积的最大值.
t-2,过D作y轴的平行线交AC于E.即可求得DE的长,继而可求得S△DCA=-(t-2)2+4,然后由二次函数的性质,即可求得点D的坐标及△DCA面积的最大值.
解:(1)将点A(4,0)、B(1,0)代入抛物线解析式得:
 ,
,
解得: ,
,
则抛物线解析式为![]() ;
;
存在.
如图1,设D点的横坐标为t(0<t<4),则D点的纵坐标为﹣![]() t2+
t2+![]() t﹣2.
t﹣2.
过D作y轴的平行线交AC于E.
设直线AC的解析式为:y=mx+n,
则 ![]() ,
,
解得: ,
,
由题意可求得直线AC的解析式为y=![]() x﹣2.
x﹣2.
∴E点的坐标为(t,![]() t﹣2).
t﹣2).
∴DE=﹣![]() t2+
t2+![]() t﹣2﹣(
t﹣2﹣(![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+2t.
t2+2t.
∴S△DCA=S△CDE+S△ADE=![]() ×DE×OA=
×DE×OA=![]() ×(﹣
×(﹣![]() t2+2t)×4=﹣t2+4t=﹣(t﹣2)2+4.
t2+2t)×4=﹣t2+4t=﹣(t﹣2)2+4.
∴当t=2时,S最大=4.
∴当D(2,1),△DAC面积的最大值为4.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
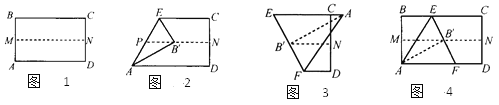
【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
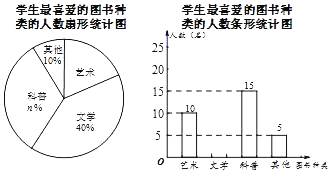
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并请根据以上信息补全条形统计图;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)根据抽样调查的结果,请你估计该校900名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
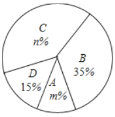
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西省相关文件规定,西安市实行居民阶梯水价制度,对居民用水的基本水价实行![]() 三级价差,各阶梯水价均为用户终端水价,具体如下:
三级价差,各阶梯水价均为用户终端水价,具体如下:
第一阶梯:年用水量![]() 及以下,终端水价为
及以下,终端水价为![]() 元/
元/![]() .
.
第二阶梯:年用水量![]() (含),终端水价为
(含),终端水价为![]() 元/
元/![]() .
.
第三阶梯:年用水量![]() 以上,终端水价为
以上,终端水价为![]() 元/
元/![]() .
.
城区居民阶梯水价计量结算周期以年为单位,年用水量累计达到各阶梯水量上限后,超出部分执行下一阶梯水价;年度周期之间水量不结转,不累计.
设某户居民2019年的年用水量为![]() ,应缴水费为
,应缴水费为![]() (元).
(元).
(1)写出该户居民2019年的年用水量为![]() 含)的
含)的![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)若该户居民2019年的应缴水费为![]() 元,则该户居民2019年的年用水量为多少.
元,则该户居民2019年的年用水量为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
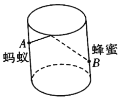
【题目】如图,圆柱形玻璃杯高为![]() ,底面周长为
,底面周长为![]() ,在杯内壁离杯底
,在杯内壁离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁上,它在离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁上,它在离杯上沿![]() 且与蜂蜜相对的
且与蜂蜜相对的![]() 处,则蚂蚁从外壁
处,则蚂蚁从外壁![]() 处走到内壁
处走到内壁![]() 处,至少爬多少厘米才能吃到蜂蜜( )
处,至少爬多少厘米才能吃到蜂蜜( )
A.24B.25C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
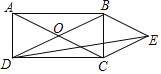
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
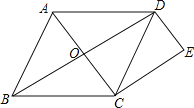
【题目】如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com