
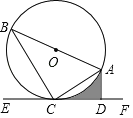
【题目】如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.
(1)求证:EF是⊙O的切线;
(2)若AD=1,求BC的长;
(3)在(2)的条件下,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OC,由OB=OC,利用等边对等角得到∠BCO=∠B,由∠ACD=∠B,得到∠ACD+∠OCA=90°,即可得到EF为圆O的切线;
(2)证明Rt△ABC∽Rt△ACD,可求出AC=2,由勾股定理求出BC的长即可;
(3)求出∠B=30°,可得∠AOC=60°,在Rt△ACD中,求出CD,然后用梯形ADCO和扇形OAC的面积相减即可得出答案.
(1)证明:连接OC,
∵AB是⊙O直径,
∴∠ACB=90°,即∠BCO+∠OCA=90°,
∵OB=OC,
∴∠BCO=∠B,
∵∠ACD=∠B,
∴∠ACD+∠OCA=90°,
∵OC是⊙O的半径,
∴EF是⊙O的切线;
(2)解:在Rt△ABC和Rt△ACD中,
∵∠ACD=∠B,∠ACB=∠ADC,
∴Rt△ABC∽Rt△ACD,
∴![]() ,
,
∴AC2=ADAB=1×4=4,
∴AC=2,
∴![]() ;
;
(3)解:∵在Rt△ABC中,AC=2,AB=4,
∴∠B=30°,
∴∠AOC=60°,
在Rt△ADC中,∠ACD=∠B=30°,AD=1,
∴CD=![]() =
=![]() =
=![]() ,
,
∴S阴影=S梯形ADCO﹣S扇形OAC=![]() .
.



科目:初中数学 来源: 题型:
【题目】下面是小如同学设计的“作已知直角三角形的外接圆”的尺规作图过程
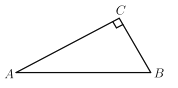
已知:![]() ,
,![]() .
.
求作:![]() 的外接圆.
的外接圆.
作法:如图,
①分别以点![]() 和
和![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
②作直线![]() ,交
,交![]() 于点
于点![]() ;
;
③以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() .
.
![]() 即为所求作的圆.
即为所求作的圆.
根据小如同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹).
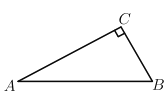
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 由作图,
由作图,![]() ,
,![]() ,
,
![]() 且
且![]() (__________)(填推理的依据).
(__________)(填推理的依据).
![]() ,
,
![]() (__________)(填推理的依据).
(__________)(填推理的依据).
![]() ,
,
![]() ,
,![]() ,
,![]() 三点在以
三点在以![]() 为圆心,
为圆心,![]() 为直径的圆上.
为直径的圆上.
![]() 为
为![]() 的外接圆.
的外接圆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式ax2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
ax2+bx+c | … | 3 |
| ﹣1 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=ax2+bx+c,则当x取何值时,y<0;
(3)当0<x<3,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目“抛物线l1:![]() (﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
(﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
A.只有甲的结果正确
B.只有乙的结果正确
C.甲、乙的结果合起来才正确
D.甲、乙的结果合起来也不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.4 | 4.3 | ||
卡路里消耗(千卡) | 157 | 79 | 91 | 127 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
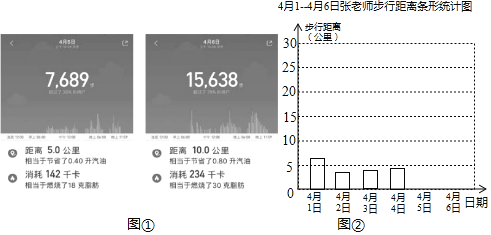
(1)请你将手环记录的4月5日和4月6日的数据(如图①)填入表格
(2)请你将条形统计图(如图②)补充完整
(3)张老师这6天平均每天步行约______公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为______公里(精确到0.1公里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
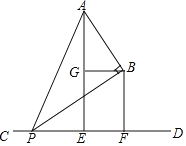
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
![]() ______,
______,![]() ______.
______.
![]() 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.
![]() 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
![]() 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com