
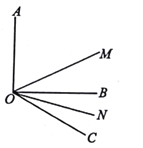
【题目】(1)如图,已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.
(2)如果(1)中,![]() ,其他条件不变,求
,其他条件不变,求![]() 的度数.
的度数.
(3)如果(1)中,![]() ,
,![]() ,其他条件不变,求
,其他条件不变,求![]() 的度数.
的度数.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
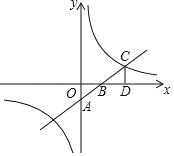
【题目】如图,一次函数 y=kx+b 的图象与坐标轴分别交于 A、B 两点,与反比例函数 y=![]() 的图象在第一象限的交点为点 C,CD⊥x 轴,垂足为点 D,若OB=3,OD=6,△AOB 的面积为 3.
的图象在第一象限的交点为点 C,CD⊥x 轴,垂足为点 D,若OB=3,OD=6,△AOB 的面积为 3.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当 x>0 时,kx+b﹣![]() >0 的解集.
>0 的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
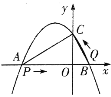
【题目】如图,已知抛物线y=-![]() 与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求b的值及点B的坐标;
(2)试判断△ABC的形状,并说明理由;
(3)一动点P从点A出发,以每秒2个单位的速度向点B运动,同时动点Q从点B出发,以每秒1个单位的速度向点C运动(当点P运动到点B时,点Q随之停止运动),设运动时间为t秒,当t为何值时,△PBQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,每辆车的月租金为4000元时,可全部租出.每辆车的月租金每增加100元,未租出的车将增加1辆.租出的车每辆每月的维护费为500元,未租出的车每辆每月只需维护费100元.
(1)当每辆车的月租金为4600元时,能租出多少辆?并计算此时租赁公司的月收益(租金收入扣除维护费)是多少万元?
(2)规定每辆车月租金不能超过7200元,当每辆车的月租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达40.4万元?
(3)当每辆车的月租金定为_________元时,租赁公司的月收益最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米处建有一个监测点P,道路AB段为检测区(如图).在△ABP中,已知∠PAB=32°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速?(精确到0.1秒.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
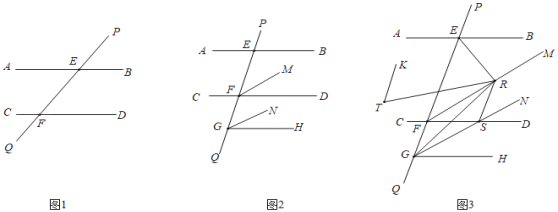
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com