
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 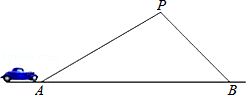
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣ ![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2= ![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m). 
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加操作技能培训,他们在培训期间参加的5次测试成绩(满分10分)记录如下:
5次测试成绩(分) | 平均数 | 方差 | |||||
甲 | 8 | 8 | 7 | 8 | 9 | 8 | 0.4 |
乙 | 5 | 9 | 7 | 10 | 9 | 8 | 3.2 |
(1)若从甲、乙两人中选派一人参加操作技能大赛,你认为应选谁?为什么?
(2)如果乙再测试一次,成绩为8分,请计算乙6次测试成绩的方差(结果保留小数点后两位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明: ![]() =
= ![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 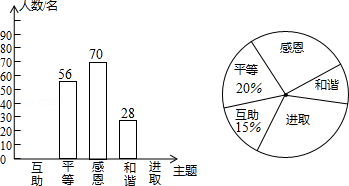
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC. 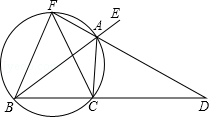
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com