
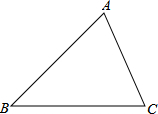
 画一条线把△ABC分成面积相等的两部分.
画一条线把△ABC分成面积相等的两部分. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
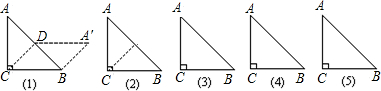
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
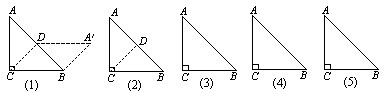
【尝试】如图,把一个等腰直角![]() ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形A ’BCD,如示意图①.(以下有画图要求的,工具不限,不必写画法和证明)
ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形A ’BCD,如示意图①.(以下有画图要求的,工具不限,不必写画法和证明)
(1)猜一猜:四边形A’BCD一定是 ;
(2)试一试:按上述的裁剪方法,请你拼一个与图①不同的四边形,并在图②中画出示意图.

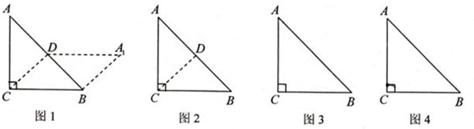
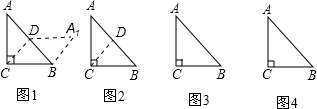
【探究】在等腰直角AABC中,请你沿任意一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)想一想:你能拼得的特殊四边形分别是 :(写出两种)
(2)画一画:请分别在图③、图④中画出你拼得的这两个特殊四边形的示意图.
【拓广】在图⑤等腰直角![]() ABC中,请你沿一条与三角形中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个直角梯形.
ABC中,请你沿一条与三角形中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个直角梯形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com