Question

设计三种不同方案，把△ABC的面积三等分．

Answer 1

解：
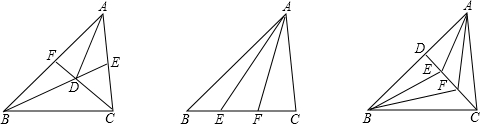
方法一：分别作出AB，AC边的中点点F，点E，连接CF，BE，CF与BE交于点D，则点D是三角形的重心，连接AD，则△ABD，△BCD，△ACD的面积分别相等；

方法二，作出BC的三等分点E，F，连接AE，AF，则△ABE，△AEF，△AFC的面积分别相等；

方法三，作出AB边上的高CD，作出CD的三等分点E，F，连接AE，AF，BE，BF，则△ABE，四边形AEBF，四边形AFBC的面积分别相等．
分析：方法一：把一边三等分，将分点与相对顶点连接，所成的三个三角形都是等底等高，所以面积相等；
方法二：画出三角形任意两条中线，取其交点．将交点与三角形三个顶点连起来；
方法三：画出三角形的高，再画出高的垂直平分线．然后三等分高，连接三等分点到两个底边的连线，则可以三等分三角形．
点评：本题利用了三角形的重心的性质，三等分线段的求作，高的求作．