
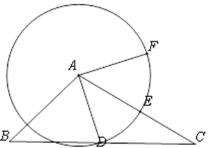
【题目】如图,已知△ABC,AB=![]() ,
,![]() ,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
(1)设BD为x,点D、F之间的距离为y,求y关于x的函数解析式,并写出定义域;
(2)如果E是![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)联结CF,如果四边形ADCF是梯形,求BD的长 .

【答案】(1) ![]() (0≤x≤3); (2)
(0≤x≤3); (2) ![]() ; (3) BD的长是1或
; (3) BD的长是1或![]() .
.
【解析】
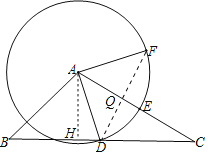
(1)过点A作AH⊥BC,垂足为点H.构造直角三角形,利用解直角三角形和勾股定理求得AD的长度.联结DF,点D、F之间的距离y即为DF的长度,在Rt△ADF中,利用锐角三角形函数的定义求得DF的长度,易得函数关系式.
(2)由勾股定理求得:AC=![]() .设DF与AE相交于点Q,通过解Rt△DCQ和Rt△AHC推知
.设DF与AE相交于点Q,通过解Rt△DCQ和Rt△AHC推知![]() .故设DQ=k,CQ=2k,AQ=DQ=k,所以再次利用勾股定理推知DC的长度,结合图形求得线段BD的长度,易得答案.
.故设DQ=k,CQ=2k,AQ=DQ=k,所以再次利用勾股定理推知DC的长度,结合图形求得线段BD的长度,易得答案.
(3)如果四边形ADCF是梯形,则需要分类讨论:①当AF∥DC、②当AD∥FC.根据相似三角形的判定与性质,结合图形解答.
(1)过点![]() 作AH⊥BC,垂足为点H.
作AH⊥BC,垂足为点H.
∵∠B=45°,AB=![]() ,∴
,∴![]() .
.
∵BD为x,∴![]() .
.
在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
联结DF,点D、F之间的距离y即为DF的长度.
∵点F在圆A上,且AF⊥AD,∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∴![]() .
.![]() ;
;
(2)∵E![]() 的中点,∴
的中点,∴![]() ,
,![]() 平分
平分![]() .
.
∵BC=3,∴![]() .∴
.∴![]() .
.
设DF与AE相交于点Q,在Rt△![]() 中,
中,![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
(3)如果四边形ADCF是梯形
则①当AF∥DC时,![]() .
.
∵![]() ,∴
,∴![]() ,即点D与点H重合. ∴
,即点D与点H重合. ∴![]() .
.
②当AD∥FC时,![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ∽
∽![]() .∴
.∴![]() .
.
∵![]() ,
,![]() .
.
∴![]() .即
.即![]() ,
,
整理得 ![]() ,解得
,解得 ![]() (负数舍去).
(负数舍去).
综上所述,如果四边形ADCF是梯形,BD的长是1或![]() .
.


科目:初中数学 来源: 题型:
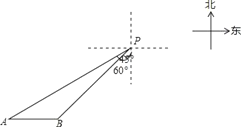
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
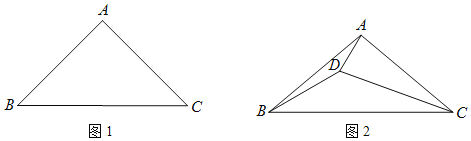
【题目】在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为α.
(1)如图,∠BAC=90°,α=45°,试求点D到边AB,AC的距离的比值;
(2)如图,∠BAC=100°,α=20°,连接AD,BD,求∠CBD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA2为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心,按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点A2019的坐标是_____.
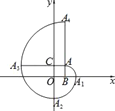
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,AD=![]() ,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,那么线段DF的长是____.(用含
,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,那么线段DF的长是____.(用含![]() 的代数式表示)
的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级积极推进走班制教学。为了了解一段时间以来,“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

“至善班”甲=乙班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

整理数据:(成绩得分用![]() 表示)
表示)
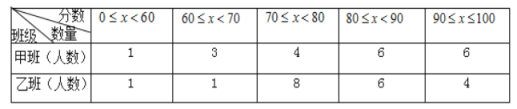
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
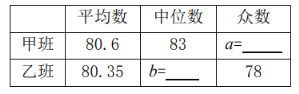
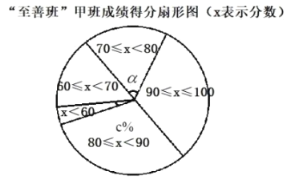
![]() 在“至善班”甲班的扇形图中,成绩在
在“至善班”甲班的扇形图中,成绩在![]() 的扇形中,说对的圆心角
的扇形中,说对的圆心角![]() 的度数为 .估计全部“至善班”的
的度数为 .估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
① .
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某底面为圆形的古塔剖面和山坡的剖面在同一平面上,古塔EF(F为塔底的中心)与地面BD垂直,古塔的底面直径CD=8米,BC=10米,斜坡AB=26米,斜坡坡面AB的坡度i=5:12,在坡脚的点A处测得古塔顶端点E的仰角∠GAE=47°,则古塔EF的高度约( )(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
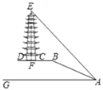
A. 27.74米B. 30.66米C. 35.51米D. 40.66米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:正方形OCAB,A(2,2),Q(5,7),AB⊥y轴,AC⊥x轴,OA,BC交于点P,若正方形OCAB以O为位似中心在第一象限内放大,点P随正方形一起运动,当PQ达到最小值时停止运动.以PQ的长为边长,向PQ的右侧作等边△PQD,求在这个位似变化过程中,D点运动的路径长( )
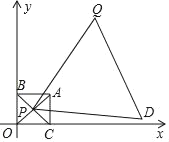
A. 5![]() B. 6C. 2
B. 6C. 2![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com