Question

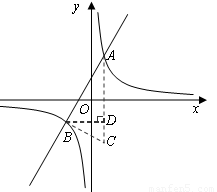
已知反比例函数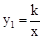的图象与一次函数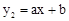的图象交于点A（1，4）和点B

（，）．

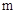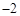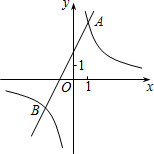
（1）求这两个函数的表达式；

（2）观察图象，当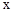>0时，直接写出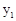>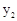时自变量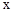的取值范围；

（3）如果点C与点A关于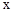轴对称，求△ABC的面积．

 

Answer 1

【答案】

解：（1）∵点A（1，4）在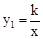的图象上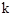，∴＝1×4＝4。

∴反比例函数的表达式为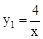 

∵点B在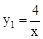的图象上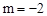，∴ 。∴点B（－2，－2）。

又∵点A、B在一次函数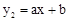的图象上，

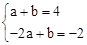∴   ，解得 。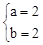

∴一次函数的表达式为。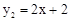 

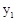（2）由图象可知，当 0＜＜1时，＞成立       

（3）∵点C与点A关于轴对称，∴C（1，－4）。

过点B作BD⊥AC，垂足为D，则D（1，－5）。  

∴△ABC的高BD＝1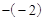＝3，底为AC＝4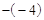＝8。

∴S_△ABC=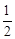AC·BD=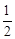×8×3=12。 

【解析】（1）根据点A的坐标求出反比例函数的解析式为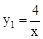，再求出B的坐标是（－2，－2），利用待定系数法求一次函数的解析式。

（2）当一次函数的值小于反比例函数的值时，直线在双曲线的下方，直接根据图象写出当>0时，一次函数的值小于反比例函数的值x的取值范围或0＜x＜1。

（3）根据坐标与线段的转换可得出：AC、BD的长，然后根据三角形的面积公式即可求出答案。