解:
(1)判断:四边形DAFE是平行四边形,
理由:∵△ABD和△BCE都是等边三角形,
∴∠DBE+∠EBA=∠ABC+∠EBA=60°
∴∠DBE=∠ABC(1.5分)
又∵BD=BA,BE=BC
∴△ABC≌△DBE
∴AC=DE=AF(2.5分)
同理△ABC≌△FEC
∴AB=EF=AD(3.5分)
∴四边形DAFE是平行四边形
(2)若四边形DAFE是矩形,则∠DAF=90°,
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAF-∠DAB-∠FAC=360°-90°-60°-60°=150°
(3)①若四边形DAFE是菱形,则AD=AE,主要可以得到:AB=AC,但不能出现AB≠BC,因为当AB=AC=BC时,△ABC是等边三角形,和△EBC就重合了.故填:AB=AC≠BC;
②当∠BAC=60°时,根据已知可以得到∠DAF=180°,那么D、A、F三点在同一条直线上,此时四边形就不成立了.
故填:∠BAC=60°,不答“≠”不得分,②∠BAC=60°
分析:(1)四边形DAFE是平行四边形,根据△ABD,△BCE和△ACF都是等边三角形容易得到全等条件证明△ABC≌△DBE,然后利用全等三角形的性质解决问题;
(2)根据(1)知道四边形DAFE是平行四边形,若四边形DAFE是矩形,则∠DAF=90°,然后根据题目已知容易求出∠BAC=150°;
(3)根据(1)知道四边形DAFE是平行四边形,若四边形DAFE是菱形,则AD=AE,主要可以得到:AB=AC,但不能出现AB≠BC,因为当AB=AC=BC时,△ABC是等边三角形,所以∠BAC=60°,此时根据已知可以得到∠DAF=180°,那么D、A、F三点在同一条直线上,此时四边形就不成立了.
点评:本题是开放题,可以结合特殊四边形的判定方法探讨不同给出的不同条件,此题要求学生对几类特殊四边形的性质与判定很熟练.

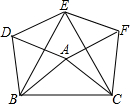 如图,△ABD,△BCE和△ACF都是等边三角形,连DE和EF.
如图,△ABD,△BCE和△ACF都是等边三角形,连DE和EF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案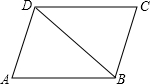 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )