
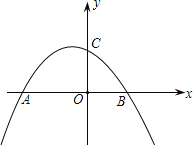
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
【答案】(1)A(﹣4,0)、B(2,0);(2)D点坐标为:D1(﹣1,![]() ),D2(﹣1,
),D2(﹣1,![]() );(3)直线l的解析式为y=
);(3)直线l的解析式为y=![]() x+3或y=
x+3或y=![]() x﹣3.
x﹣3.
【解析】
解:(1)在![]() 中,令y=0,即
中,令y=0,即![]() ,解得x1=﹣4,x2=2.
,解得x1=﹣4,x2=2.
∵点A在点B的左侧,∴A、B点的坐标为A(﹣4,0)、B(2,0).
(2)由![]() 得,对称轴为x=﹣1.
得,对称轴为x=﹣1.
在![]() 中,令x=0,得y=3.
中,令x=0,得y=3.
∴OC=3,AB=6,![]() .
.
在Rt△AOC中,![]() .
.
设△ACD中AC边上的高为h,则有![]() ACh=9,解得h=
ACh=9,解得h=![]() .
.
如图1,在坐标平面内作直线平行于AC,且到AC的距离=h=![]() ,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D.
,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D.
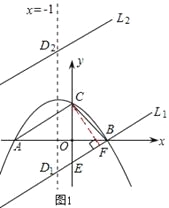
设L1交y轴于E,过C作CF⊥L1于F,则CF=h=![]() ,
,
∴ .
.
设直线AC的解析式为y=kx+b,
将A(﹣4,0),B(0,3)坐标代入,得
![]() ,解得
,解得![]() .
.
∴直线AC解析式为![]() .
.
直线L1可以看做直线AC向下平移CE长度单位(![]() 个长度单位)而形成的,
个长度单位)而形成的,
∴直线L1的解析式为![]() .
.
则D1的纵坐标为![]() .∴D1(﹣1,
.∴D1(﹣1,![]() ).
).
同理,直线AC向上平移![]() 个长度单位得到L2,可求得D2(﹣1,
个长度单位得到L2,可求得D2(﹣1,![]() ).
).
综上所述,D点坐标为:D1(﹣1,![]() ),D2(﹣1,
),D2(﹣1,![]() ).
).
(3)如图2,以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N.
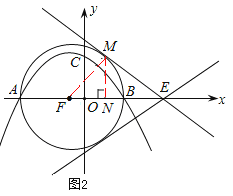
∵A(﹣4,0),B(2,0),∴F(﹣1,0),⊙F半径FM=FB=3.
又FE=5,则在Rt△MEF中,ME=![]() ,sin∠MFE=
,sin∠MFE=![]() ,cos∠MFE=
,cos∠MFE=![]() .
.
在Rt△FMN中,MN=MFsin∠MFE=3×![]() ,FN=MFcos∠MFE=3×
,FN=MFcos∠MFE=3×![]() .
.
则ON=![]() .
.
∴M点坐标为(![]() ,
,![]() ).
).
直线l过M(![]() ,
,![]() ),E(4,0),
),E(4,0),
设直线l的解析式为y=k1x+b1,则有 ,解得
,解得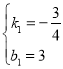 .
.
∴直线l的解析式为y=![]() x+3.
x+3.
同理,可以求得另一条切线的解析式为y=![]() x﹣3.
x﹣3.
综上所述,直线l的解析式为y=![]() x+3或y=
x+3或y=![]() x﹣3.
x﹣3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“自主互助学习型课堂竞赛”中,为奖励表现突出的同学,初一(7)班利用班费![]() 元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买
元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买![]() 支,若钢笔每支
支,若钢笔每支![]() 元,相册每本
元,相册每本![]() 元,笔记本每本
元,笔记本每本![]() 元,在把钱都用尽的条件下,买法共有( )
元,在把钱都用尽的条件下,买法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:初中数学 来源: 题型:
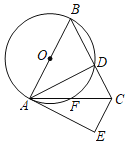
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,且∠CAD=∠CAE.
(1)求证:AE是⊙O的切线;
(2)若AB=8,AC=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
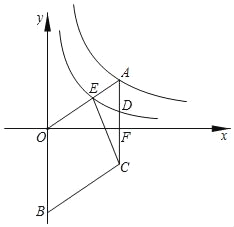
【题目】如图所示,菱形AOBC的顶点B在y轴上,顶点A在反比例函数y=![]() 的图象上,边AC,OA分别交反比例函数y=
的图象上,边AC,OA分别交反比例函数y=![]() 的图象于点D,点E,边AC交x轴于点F,连接CE.已知四边形OBCE的面积为12,sin∠AOF=
的图象于点D,点E,边AC交x轴于点F,连接CE.已知四边形OBCE的面积为12,sin∠AOF=![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“停课不停学”过程中学生对网课内容的喜爱程度,某校开展了一次网上问卷调查.随机抽取部分学生,按四个类别统计,其中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,并将调查结果绘制成下面两幅不完整的统计图.
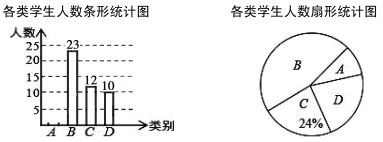
请根据图中提供的信息,解决下列问题:
(1)这次共抽取 名学生进行统计调查,扇形统计图中D类所在扇形的圆心角度数为 ;
(2) 将条形统计图补充完整;
(3) 若该校共有3000名学生,估计该校表示“喜欢”的B类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
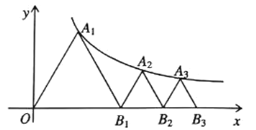
【题目】如图,已知等边三角形![]() ,顶点
,顶点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 的坐标为
的坐标为![]() .过
.过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]()
![]() 交
交![]() 轴于点
轴于点![]() ,得到第二个等边
,得到第二个等边![]() ;过
;过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,得到第三个等边
,得到第三个等边![]() ;以此类推,... 则点
;以此类推,... 则点![]() 的坐标为____.
的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论![]() 为任何实数,此方程总有两个实数根;
为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为![]() 、
、![]() ,满足
,满足![]() ,求
,求![]() 的值;
的值;
(3)若![]() △
△![]() 的斜边为5,另外两条边的长恰好是方程的两个根
的斜边为5,另外两条边的长恰好是方程的两个根![]() 、
、![]() ,求
,求![]()
![]() 的内切圆半径.
的内切圆半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com