
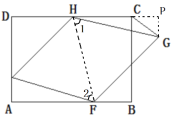
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDЃЌDCЃН8ЃЌADЃН6.
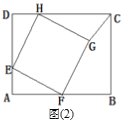
(1)ШчЭМ(1)ЃЌЕуEдкБпADЩЯЧвAEЃН2ЃЌвдЕуEЮЊЖЅЕузїе§ЗНаЮEFGHЃЌЖЅЕуFЃЌHЗжБ№дкОиаЮABCDЕФБпABЃЌCDЩЯЃЌСЌНгCGЃЌЧѓЁЯHCGЕФЖШЪ§ЃЛ
(2)ЧыДгAЁЂBСНЬтжаШЮбЁвЛЬтНтД№ЃЌЮвбЁдё_____.
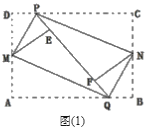
A.ШчЭМ(2)ЃЌМзЭЌбЇАбОиаЮжНЦЌABCDЕФЫФИіНЧЯђФкелЦ№ЃЌЧЁКУЦДГЩвЛИіЮоЗьЯЖЮожиЕўЕФЫФБпаЮMPNQЃЌХаЖЯВЂЫЕУїЫФБпаЮMPNQЕФаЮзД.
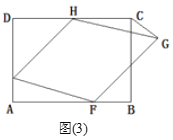
B.ШчЭМ(3)ЃЌввЭЌбЇАб(1)жаЕФЁАе§ЗНаЮEFGHЁБИФЮЊЁАСтаЮEFGHЁБЃЌЦфгрЬѕМўВЛБфЃЌДЫЪБЕуGТфдкОиаЮABCDЕФЭтВПЃЌвбжЊЁїCGHЕФУцЛ§ЪЧ4ЃЌЧѓСтаЮEFGHЕФБпГЄМАУцЛ§.
ЁОД№АИЁП(1)ЁЯHCG= 45ЁуЃЛ(2)AЃКЫФБпаЮMPNQЕФаЮзДЪЧОиаЮЃЌжЄУїМћНтЮіЃЛBЃКСтаЮEFGHЕФБпГЄМАУцЛ§ЗжБ№ЮЊ4![]() КЭ8+8
КЭ8+8![]() .
.
ЁОНтЮіЁП
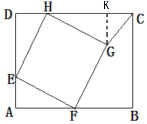
ЃЈ1ЃЉЯШИљОнЬѕМўХаЖЈЁїAFEЁеЁїDEHЁеЁїKHGЃЌЕУГіAE=DH=GK=2ЃЌDE=HKЃЌНјЖјЕУГіGK=CKЃЌМДЁїCGKЮЊЕШбќжБНЧШ§НЧаЮЃЌОнДЫЕУГіЁЯHCGЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЂйШєбЁAЬтЃЌдђИљОнелЕўЕФаджЪЃЌЧѓЕУЁЯPMQ=ЁЯPME+ЁЯQME=1212ЁЯDME+1212ЁЯAME=1212ЁЯAMD=90ЁуЃЌЭЌРэПЩЕУЃЌЁЯMQN=90ЁуЃЌЁЯPNQ=90ЁуЃЌНјЖјЕУГіЫФБпаЮMPNQЕФаЮзДЪЧОиаЮЃЛ
ЂкШєбЁBЬтЃЌдђашвЊСЌНгHFЃЌЙ§GзїGPЁЭCDЕФбгГЄЯпгкPЃЌдйИљОнОиаЮКЭСтаЮЕФаджЪЃЌХаЖЈЁїAEFЁеЁїPGHЃЈAASЃЉЃЌЕУГіPG=AE=2ЃЌдйИљОнЁїCGHЕФУцЛ§ЪЧ4ЃЌЧѓЕУCHЕФГЄЃЌНјЖјдкRtЁїDEHжаЃЌИљОнЙДЙЩЖЈРэЕУГіEHЃЌМДЕУГіСтаЮEFGHЕФБпГЄЃЌзюКѓИљОнСтаЮEFGHЕФУцЛ§=2ЁСЁїEFHЕФУцЛ§=2ЁСЃЈЫФБпаЮADHFЕФУцЛ§-ЁїDEHЕФУцЛ§-ЁїAEFЕФУцЛ§ЃЉЃЌНјааМЦЫуЧѓНтМДПЩЃЎ
(1)Й§ЕуGзїGKЁЭCDгкЕуKЃЌ
ЁпЫФБпаЮABCDЮЊОиаЮЃЌDCЃН8ЃЌADЃН6ЃЌ
ЁрЁЯAЃНЁЯDЃНЁЯHKGЃН90ЁуЃЌ
ЁпЫФБпаЮEFGHЮЊе§ЗНаЮЃЌ
ЁрЁЯFEHЃНЁЯEHGЃН90ЁуЃЌEFЃНEHЃНHGЃЌ
ЁрЁЯAFEЃНЁЯDEHЃНЁЯKHGЃЌ
ЁрЁїAFEЁеЁїDEHЁеЁїKHGЃЌ
ЁрAEЃНDHЃНGKЃН2ЃЌDEЃНHKЃЌ
ЁпDCЃН8ЃЌADЃН6ЃЌ
ЁрCKЃНDCЉDHЃН8Љ6ЃН2ЃЌ
ЁрGKЃНCKЃЌ
ЁрЁЯKCGЃНЁЯCGKЃН45ЁуЃЌМДЁЯHCGЕФЖШЪ§ЪЧ45ЁуЃЛ
(2)бЁAЬтЃЌЫФБпаЮMPNQЕФаЮзДЪЧОиаЮ.жЄУїЃКШчЭМ2ЃЌ
ЁпЫФБпаЮABCDЮЊОиаЮЃЌ
ЁрЁЯAЃНЁЯDЃН90ЁуЃЌ
ЁпDMгыEMжиКЯЃЌAMгыEMжиКЯЃЌ
ЁрPMЦНЗжЁЯDMEЃЌQMЦНЗжЁЯAMEЃЌ
ЁрЁЯPMQЃНЁЯPME+ЁЯQMEЃН![]() ЁЯDME+
ЁЯDME+![]() ЁЯAMEЃН
ЁЯAMEЃН![]() ЁЯAMDЃН90ЁуЃЌ
ЁЯAMDЃН90ЁуЃЌ
ЭЌРэПЩЕУЃЌЁЯMQNЃН90ЁуЃЌЁЯPNQЃН90ЁуЃЌ
ЁрЫФБпаЮMPNQЕФаЮзДЪЧОиаЮ.
бЁBЬтЃЌШчЭМ3ЃЌСЌНгHFЃЌЙ§GзїGPЁЭCDЕФбгГЄЯпгкPЃЌЁпЫФБпаЮABCDЮЊОиаЮЃЌЁрABЁЮCDЃЌЁЯAЃНЁЯDЃН90ЁуЃЌЁрЁЯAFHЃНЁЯPHFЃЌ
ЁпЫФБпаЮEFGHЮЊСтаЮЃЌ
ЁрEFЁЮHGЃЌEFЃНHGЃЌ
ЁрЁЯ1ЃНЁЯ2ЃЌ
ЁрЁЯAFEЃНЁЯPHGЃЌ
гжЁпGPЁЭDPЃЌ
ЁрЁЯPЃНЁЯAЃН90ЁуЃЌ
ЁрЁїAEFЁеЁїPGH(AAS)ЃЌ
ЁрPGЃНAEЃН2ЃЌ
ЁпЁїCGHЕФУцЛ§ЪЧ4ЃЌ
Ёр![]() ЁСHCЁСPGЃН4ЃЌ
ЁСHCЁСPGЃН4ЃЌ
ЁрHCЃН4ЃЌ
ЁпCDЃН8ЃЌADЃН6ЃЌAEЃН2ЃЌ
ЁрDHЃН8Љ4ЃН4ЃЌDEЃН6Љ2ЃН4ЃЌ
ЁрRtЁїDEHжаЃЌEHЃН4![]() ЃЌ
ЃЌ
ЁрEFЃН4![]() ЃЌМДСтаЮEFGHЕФБпГЄЮЊ4
ЃЌМДСтаЮEFGHЕФБпГЄЮЊ4![]() ЃЌ
ЃЌ
ЁрRtЁїAEFжаЃЌAFЃН2![]() ЃЌ
ЃЌ
ЁрСтаЮEFGHЕФУцЛ§ЃН2ЁСЁїEFHЕФУцЛ§
ЃН2ЁС(ЫФБпаЮADHFЕФУцЛ§ЉЁїDEHЕФУцЛ§ЉЁїAEFЕФУцЛ§)
ЃН2ЁС[![]() (DH+AF)ЁСADЉ
(DH+AF)ЁСADЉ![]() ЁСDHЁСEDЉ
ЁСDHЁСEDЉ![]() ЁСAEЁСAF]
ЁСAEЁСAF]
ЃН8+8![]() .
.
ЁрСтаЮEFGHЕФБпГЄМАУцЛ§ЗжБ№ЮЊ4![]() КЭ8+8
КЭ8+8![]() .
.


 бЇСЗПьГЕЕРПьРжМйЦкЪюМйзївЕаТНЎШЫУёГіАцЩчЯЕСаД№АИ
бЇСЗПьГЕЕРПьРжМйЦкЪюМйзївЕаТНЎШЫУёГіАцЩчЯЕСаД№АИ еуДѓгХбЇаЁбЇФъМЖЯЮНгЕМгыСЗеуНДѓбЇГіАцЩчЯЕСаД№АИ
еуДѓгХбЇаЁбЇФъМЖЯЮНгЕМгыСЗеуНДѓбЇГіАцЩчЯЕСаД№АИ аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ
аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ
ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌ![]() ЕФЖЅЕуОљдкИёЕуЩЯЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
ЕФЖЅЕуОљдкИёЕуЩЯЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() .
.
ЃЈ1ЃЉНЋ![]() Йигк
Йигк![]() жсзїжсЖдГЦБфЛЛЕУ
жсзїжсЖдГЦБфЛЛЕУ![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ______.
ЕФзјБъЮЊ______.
ЃЈ2ЃЉНЋ![]() ШЦдЕу
ШЦдЕу![]() АДФцЪБеыЗНЯђа§зЊ
АДФцЪБеыЗНЯђа§зЊ![]() ЕУ
ЕУ![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ______.
ЕФзјБъЮЊ______.
ЃЈ3ЃЉдкЃЈ1ЃЉЃЈ2ЃЉЕФЛљДЁЩЯЃЌЭМжаЕФ![]() ЃЌ
ЃЌ![]() ЪЧжааФЖдГЦЭМаЮЃЌЖдГЦжааФЕФзјБъЮЊ______.
ЪЧжааФЖдГЦЭМаЮЃЌЖдГЦжааФЕФзјБъЮЊ______.
ЃЈ4ЃЉШєвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌжБНгаДГіЕу![]() ЕФзјБъЮЊ______.
ЕФзјБъЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
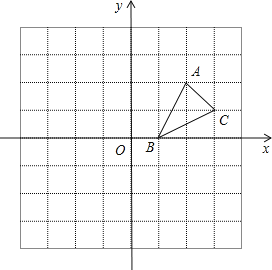
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЪЧAЃЈ1ЃЌ1ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЌCЃЈ3ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCЯђЯТЦНвЦ5ИіЕЅЮЛКѓЕУЕНЁїA1B1C1ЃЌЧыЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉНЋЁїABCШЦдЕуOФцЪБеыа§зЊ90ЁуКѓЕУЕНЁїA2B2C2ЃЌЧыЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉХаЖЯвдOЃЌA1ЃЌBЮЊЖЅЕуЕФШ§НЧаЮЕФаЮзДЃЎЃЈЮоаыЫЕУїРэгЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
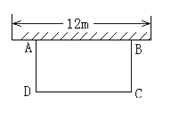
ЁОЬтФПЁПШчЭМЃЌПЦММаЁзщзМБИгУВФСЯЮЇНЈвЛИіУцЛ§ЮЊ60m2ЕФОиаЮПЦММдАABCDЃЌЦфжавЛБпABППЧНЃЌЧНГЄЮЊ12mЃЌЩшADЕФГЄЮЊ![]() mЃЌDCЕФГЄЮЊ
mЃЌDCЕФГЄЮЊ![]() mЁЃ
mЁЃ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИљОнЪЕМЪЧщПіЃЌЖдгкЃЈ1ЃЉЪНжаЕФКЏЪ§здБфСП![]() ФмЗёШЁжЕЮЊ4mЃЌШєФмЃЌЧѓГі
ФмЗёШЁжЕЮЊ4mЃЌШєФмЃЌЧѓГі![]() ЕФжЕЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЕФжЕЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЮЇГЩОиаЮПЦММдАABCDЕФШ§БпВФСЯзмГЄВЛГЌЙ§26mЃЌВФСЯADКЭDCЕФГЄЖМЪЧећУзЪ§ЃЌЧѓГіТњзуЬѕМўЕФЫљгаЮЇНЈЗНАИЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
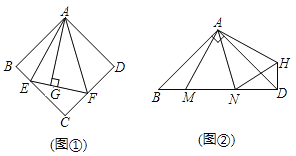
ЁОЬтФПЁП![]() ШчЭМ
ШчЭМ![]() ЃЌдке§ЗНаЮABCDжаЃЌ
ЃЌдке§ЗНаЮABCDжаЃЌ![]() ЕФЖЅЕуEЃЌFЗжБ№дкBCЃЌCDБпЩЯЃЌИпAGгые§ЗНаЮЕФБпГЄЯрЕШЃЌЧѓ
ЕФЖЅЕуEЃЌFЗжБ№дкBCЃЌCDБпЩЯЃЌИпAGгые§ЗНаЮЕФБпГЄЯрЕШЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
![]() ШчЭМ
ШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуMЃЌNЪЧBDБпЩЯЕФШЮвтСНЕуЃЌЧв
ЃЌЕуMЃЌNЪЧBDБпЩЯЕФШЮвтСНЕуЃЌЧв![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕуAФцЪБеыа§зЊ
ШЦЕуAФцЪБеыа§зЊ![]() жС
жС![]() ЮЛжУЃЌСЌНгNHЃЌЪдХаЖЯMNЃЌNDЃЌDHжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЮЛжУЃЌСЌНгNHЃЌЪдХаЖЯMNЃЌNDЃЌDHжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
![]() дкЭМ
дкЭМ![]() жаЃЌСЌНгBDЗжБ№НЛAEЃЌAFгкЕуMЃЌNЃЌШє
жаЃЌСЌНгBDЗжБ№НЛAEЃЌAFгкЕуMЃЌNЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓAGЃЌMNЕФГЄЃЎ
ЃЌЧѓAGЃЌMNЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯп
жаЃЌХзЮяЯп![]() гы
гы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]()
(1)ЧѓХзЮяЯпЕФЖЅЕузјБъЃЛ
(2)Шє![]() ЃЌ
ЃЌ
ЂйЧѓХзЮяЯпЕФНтЮіЪНЃЛ
Ђк)вбжЊЕу![]() ,
,![]() ЃЌНЋХзЮяЯпдк
ЃЌНЋХзЮяЯпдк![]() ЕФВПЗжЯђЩЯЦНвЦ
ЕФВПЗжЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕУЕНЭМЯѓ
ИіЕЅЮЛЕУЕНЭМЯѓ![]() ЃЌШєЭМЯѓ
ЃЌШєЭМЯѓ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЧЁга
ЧЁга![]() ИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі
ИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=-x2+2x+m+1НЛxжсгкЕуA(a,0ЃЉКЭB(b,0ЃЉЃЌНЛyжсгкЕуCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЯТСаЫФИіХаЖЯЃКЂйЕБx>0ЪБЃЌy>0ЃЛЂкШєa=-1ЃЌдђb=3ЃЛЂлХзЮяЯпЩЯгаСНЕуP(x1ЃЌy1ЃЉКЭQЃЈx2ЃЌy2ЃЉЃЌШєx1<1<x2ЃЌЧвx1+x2>2ЃЌдђy1>y2ЃЛЂмЕуCЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊEЃЌЕуGЁЂFЗжБ№дкxжсКЭyжсЩЯЃЌЕБm=2ЪБЃЌЫФБпаЮEDGFжмГЄЕФзюаЁжЕЮЊ![]() ЃЌЦфжаЃЌХаЖЯе§ШЗЕФађКХЪЧЃЈ ЃЉ
ЃЌЦфжаЃЌХаЖЯе§ШЗЕФађКХЪЧЃЈ ЃЉ
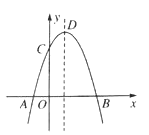
A.ЂйЂкB.ЂкЂлC.ЂйЂлD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАрЪ§бЇаЫШЄаЁзщОЙ§ЪаГЁЕїВщЃЌећРэГіФГжжЩЬЦЗдкЕк![]() ЬьЕФЪлМлгыЯњСПЕФЯрЙиаХЯЂШчЯТБэЃК
ЬьЕФЪлМлгыЯњСПЕФЯрЙиаХЯЂШчЯТБэЃК
ЙлВьБэИёЃКИљОнБэИёНтД№ЯТСаЮЪЬтЃК
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
ЃЈ1ЃЉ![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
ЃЈ2ЃЉдкЯТЭМЕФжБНЧзјБъЯЕжаЛГіКЏЪ§![]() ЕФЭМЯѓЃЌВЂИљОнЭМЯѓЃЌжБНгаДГіЕБ
ЕФЭМЯѓЃЌВЂИљОнЭМЯѓЃЌжБНгаДГіЕБ![]() ШЁЪВУДЪЕЪ§ЪБЃЌВЛЕШЪН
ШЁЪВУДЪЕЪ§ЪБЃЌВЛЕШЪН![]() ГЩСЂЃЛ
ГЩСЂЃЛ

ЃЈ3ЃЉИУЭМЯѓгы![]() жсСННЛЕуДгзѓЕНгввРДЮЗжБ№ЮЊ
жсСННЛЕуДгзѓЕНгввРДЮЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌгы
ЃЌгы![]() жсНЛЕуЮЊ
жсНЛЕуЮЊ![]() ЃЌЧѓЙ§етШ§ИіЕуЕФЭтНгдВЕФАыОЖ.
ЃЌЧѓЙ§етШ§ИіЕуЕФЭтНгдВЕФАыОЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
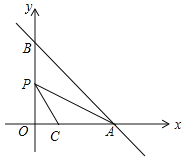
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=Љx+mЗжБ№НЛxжсЃЌyжсгкAЃЌBСНЕуЃЌвбжЊЕуCЃЈ2ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЕБжБЯпABОЙ§ЕуCЪБЃЌЕуOЕНжБЯпABЕФОрРыЪЧ ЃЛ
ЃЈ2ЃЉЩшЕуPЮЊЯпЖЮOBЕФжаЕуЃЌСЌНсPAЃЌPCЃЌШєЁЯCPA=ЁЯABOЃЌдђmЕФжЕЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com