
【题目】如图,长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发(不含点A),沿A→B→C→D运动,同时,点Q从点B出发(不含点B),沿B→C→D运动,当点P到达点B时,点Q恰好到达点C,已知点P每秒比点Q每秒多运动1cm,当其中一点到达点D(不含点D)时,另一点停止运动.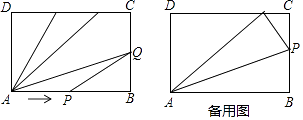
(1)求P、Q两点的速度;
(2)当其中一点到达点D时,另一点距离D点 cm(直接写答案);
(3)设点P、Q的运动时间为t(x),请用含t的代数式表示△APQ的面积为S(cm3),并写出t的取值范围.
【答案】
(1)
解:∵当点P到达点B时,点Q恰好到达点C,
∴P、Q两点的速度之比为:6:4=3:2,
设点P的速度是3xcm/s,则点Q的速度是2xcm/s,
由题意得,3x﹣2x=1,
解得,x=1,
∴点P的速度是3cm/s,则点Q的速度是2cm/s
(2)1
(3)
解:当0≤t≤2时,AP=3t,BQ=2t,
∴△APQ的面积为S= ![]() ×AP×BQ=3t2,
×AP×BQ=3t2,
当2<t≤ ![]() 时,BP=3t﹣6,CP=10﹣3t,CQ=2t﹣4,QD=10﹣2t,
时,BP=3t﹣6,CP=10﹣3t,CQ=2t﹣4,QD=10﹣2t,
∴△APQ的面积为S=6×4﹣ ![]() ×6×(3t﹣6)﹣
×6×(3t﹣6)﹣ ![]() ×4×(10﹣2t)﹣
×4×(10﹣2t)﹣ ![]() ×(10﹣3t)×(2t﹣4)=3t2﹣21t+42,
×(10﹣3t)×(2t﹣4)=3t2﹣21t+42,
当 ![]() <t≤5时,PQ=6﹣(3t﹣10)﹣[6﹣(2t﹣4)]=6﹣t,
<t≤5时,PQ=6﹣(3t﹣10)﹣[6﹣(2t﹣4)]=6﹣t,
∴△APQ的面积为S= ![]() ×PQ×AD=12﹣2t
×PQ×AD=12﹣2t
【解析】(2)点P到达点D所需的时间为:(6+4+6)÷3= ![]() s,
s,
点Q到达点D所需的时间为:(6+4)÷2=5s,
∴点Q先到达点D,
则点P距离D点16﹣3×5=1cm,
所以答案是:1;
【考点精析】关于本题考查的等腰直角三角形和翻折变换(折叠问题),需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.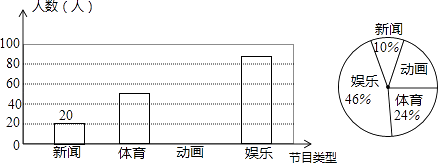
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“作差法”是常见的比较代数式大小的一种方法,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.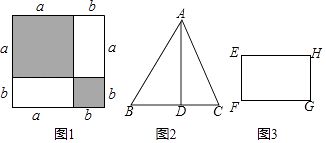
(1)如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较来两个小正方形面积之和M与两个长方形面积之和N的大小.
(2)如图2,图3,△ABC中,AD⊥BC于D,AD=BC=2x﹣y,长方形EFGH中,长EH=2x﹣ ![]() y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x>
y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x> ![]() y且x≠y.
y且x≠y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )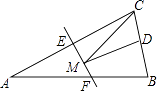
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°. 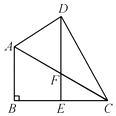
(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com