
【题目】已知:抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线y=﹣x+3经过B、C两点
(1)填空:b= (用含有a的代数式表示);
(2)若a=﹣1
①点P为抛物线上一动点,过点P作PM∥y轴交直线y=﹣x+3于点M,当点P在第一象限内时,是否存在一点P,使△PCB面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
②当m≤x≤m+3时,y的取值范围是2m≤y≤4,求m的值.
【答案】(1)﹣3a﹣1;(2)①P(![]() ,
,![]() );②m的值为0或﹣
);②m的值为0或﹣![]() .
.
【解析】
(1)直线经过B、C两点,先求出两点坐标,再带入抛物线解析式中求出表达式,然后再得到结果(2)若a=-1时,先写出抛物线解析式,然后根据条件求点P的坐标,再根据已知的m的范围,对照函数图象,求出m的值.
解:(1)直线y=﹣x+3,当y=0时,x=3;当x=0时,y=3,
∴B(3,0)、C(0,3),
∵抛物线过B(3,0)、C(0,3),
∴![]() 解得:b=﹣3a﹣1,
解得:b=﹣3a﹣1,
故答案为﹣3a﹣1.
(2)若a=﹣1,则抛物线的解析式为y=﹣x2+2x+3;
①假设存在点P(x,﹣x2+2x+3)使得△PCB的面积最大,
∴M(x,﹣x+3),
∴PM=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,
∵S△ABP=S△PMC+S△PMB=![]() PMOB=
PMOB=![]() (﹣x2+3x)×3=﹣
(﹣x2+3x)×3=﹣![]() (x2﹣3x)
(x2﹣3x)
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
当点P(![]() ,
,![]() )在第一象限,此时△PBC的面积最大,
)在第一象限,此时△PBC的面积最大,
故存在点P的坐标为:P(![]() ,
,![]() ),△PBC的面积最大.
),△PBC的面积最大.
②∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的开口向下,对称轴为直线x=1,有最大值4,
∴由题意可知m≤1,m+3≥1
当m=﹣![]() 是x=m和m+3对应的函数值相等,
是x=m和m+3对应的函数值相等,
当﹣![]() <m<1时,2m=﹣(m+3)2+2(m+3)+3,
<m<1时,2m=﹣(m+3)2+2(m+3)+3,
解得m1=0,m2=﹣6(不合题意舍去),
当﹣2<m<﹣![]() 时,﹣m2+2m+3=2m,
时,﹣m2+2m+3=2m,
∴m=![]() (舍)或m=﹣
(舍)或m=﹣![]()
故m的值为0或﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在![]() 点测得海岛
点测得海岛![]() 位于北偏东
位于北偏东![]() 的方向,前进
的方向,前进![]() 海里到达
海里到达![]() 点,此时,测得海岛
点,此时,测得海岛![]() 位于北偏东
位于北偏东![]() 的方向,则海岛
的方向,则海岛![]() 到航线
到航线![]() 的距离
的距离![]() 等于________海里.
等于________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
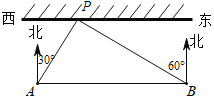
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
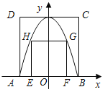
【题目】如图,正方形![]() 的顶点
的顶点![]() ,
,![]() 与正方形
与正方形![]() 的顶点
的顶点![]() ,
,![]() 同在一段抛物线上,且抛物线的顶点同时落在
同在一段抛物线上,且抛物线的顶点同时落在![]() 和
和![]() 轴上,正方形边
轴上,正方形边![]() 与
与![]() 同时落在
同时落在![]() 轴上,若正方形
轴上,若正方形![]() 的边长为
的边长为![]() ,则正方形
,则正方形![]() 的边长为________.
的边长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
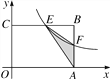
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某船以每小时![]() 海里的速度向正东方向航行,在点
海里的速度向正东方向航行,在点![]() 测得某岛
测得某岛![]() 在北偏东
在北偏东![]() 方向上,航行半小时后到达点
方向上,航行半小时后到达点![]() 测得该岛在北偏东
测得该岛在北偏东![]() 方向上,已知该岛周围
方向上,已知该岛周围![]() 海里内有暗礁.
海里内有暗礁.

![]() 说明点
说明点![]() 是否在暗礁区域内;
是否在暗礁区域内;
![]() 若继续向东航行有无触礁的危险?请说明理由.
若继续向东航行有无触礁的危险?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com