
【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠BAO=30°,AB=BO,反比例函数y=![]() (x<0)的图象经过点A
(x<0)的图象经过点A
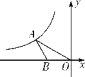
(1)求∠AOB的度数
(2)若OA=![]() ,求点A的坐标
,求点A的坐标
(3)若S△ABO=![]() ,求反比例函数的解析式
,求反比例函数的解析式
【答案】(1)30°;(2)A(﹣6,![]() );(3)
);(3)![]()
【解析】
(1)由题意直接根据等腰三角形的性质进行分析即可;
(2)由题意过点A作AC⊥x轴于点C,由∠AOB=30°,解直角三角形可得出AC=2![]() ,再由锐角三角函数或勾股定理得出OC=6,即可求得A点的坐标;
,再由锐角三角函数或勾股定理得出OC=6,即可求得A点的坐标;
(3)根据题意设OB=AB=m,根据BA=BO可得出∠ABC=60°,由此可得出AC=![]() m,由S△ABO=
m,由S△ABO=![]() ,列出关于m的方程,解方程求得m的值,进而AC和OC,结合反比例函数系数k的几何意义求得解析式.
,列出关于m的方程,解方程求得m的值,进而AC和OC,结合反比例函数系数k的几何意义求得解析式.
解(1)∵AB=BO,∠BAO=30°,
∴∠AOB=∠BAO=30°.
(2)过点A作AC⊥x轴,
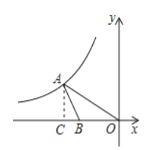
∵![]()
∴![]() ,
,
∴A(﹣6,![]() ).
).
(3)设OB=AB=![]() ,
,
得出∠ABC=60°,
在直角三角形ACB中得出AC=![]() ,
,
∵S△ABO=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AC=![]() =
=![]() ,
,
![]()
![]()
∴A(﹣3,![]() ).
).
把A点坐标代入得反比例函数的解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,以点
,以点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转135°,得到线段
顺时针旋转135°,得到线段![]() ,连接
,连接![]() .
.
(1)依题意,补全图形;
(2)求证:![]() ;
;
(3)点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 是点
是点![]() 关于点
关于点![]() 的对称点,写出
的对称点,写出![]() 的一个值,使得对任意的点
的一个值,使得对任意的点![]() 总有
总有![]() ,并证明.
,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】油井A位于油库P南偏东75°方向,主输油管道AP=12km,一新建油井B位于点P的北偏东75°方向,且位于点A的北偏西15°方向.
(1)求∠PBA;
(2)求A,B间的距离;
(3)要在AP上选择一个支管道连接点C,使从点B到点C处的支输油管道最短,求这时BC的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图,填表后再回答问题:
(1)在横线上填入正确的数:
![]() 的个数:8,______ ,24
的个数:8,______ ,24![]()
★的个数:1,4,______ ![]()
(2)试求第6个图形中“![]() ”的个数和“
”的个数和“![]() ”的个数?
”的个数?
(3)试求第108个图形中“![]() ”的个数与“
”的个数与“![]() ”的个数之差?
”的个数之差?

查看答案和解析>>
科目:初中数学 来源: 题型:
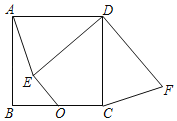
【题目】如图,正方形ABCD中,AB=2![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:

(1)根据上图求出下表所缺数据;
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 10 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
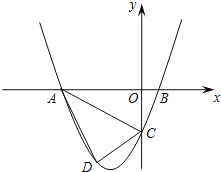
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.
(1)求证:FG与⊙O相切;
(2)连接EF,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com