
【题目】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
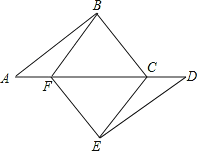
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由AB=DE,∠A=∠D,AF=DC,易证得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形;
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值.
试题解析:(1)证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
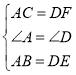 ,
,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形.
(2)解:连接BE,交CF于点G,
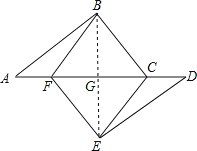
∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形,
∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() =5,
=5,
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,
∴△ABC∽△BGC,
∴![]() ,
,
即![]() ,
,
∴CG=![]() ,
,
∵FG=CG,
∴FC=2CG=![]() ,
,
∴AF=AC-FC=5-![]() =
=![]() ,
,
∴当AF=![]() 时,四边形BCEF是菱形.
时,四边形BCEF是菱形.


科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题:
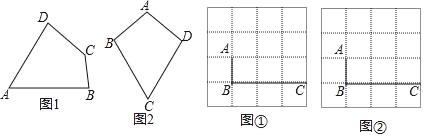
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °
(2)在探究等对角四边形性质时:
小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.
要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
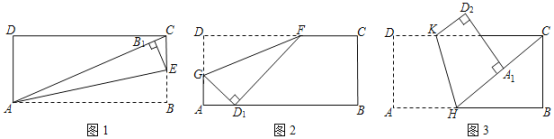
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
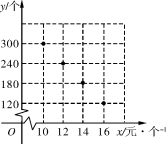
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:
(1) ![]() 与
与![]() 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,每个小方格都是边长为![]() 的正方形,
的正方形,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标是
的坐标是![]() .
.
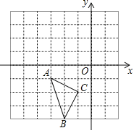
![]() 先将
先将![]() 沿
沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向向左平移
轴负方向向左平移![]() 个单位长度得到
个单位长度得到![]() ,画出
,画出![]() ,点
,点![]() 坐标是________;
坐标是________;
![]() 将
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,画出
,画出![]() ,并求出点
,并求出点![]() 的坐标是________;
的坐标是________;
![]() 我们发现点
我们发现点![]() 、
、![]() 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出一个问题“用直尺和圆规作以AB为底的等腰直角三角形ABC”.
小美的作法如下:
①分别以点A,B为圆心,大于![]() AB作弧,交于点M,N;
AB作弧,交于点M,N;
②作直线MN,交AB于点O;
③以点O为圆心,OA为半径,作半圆,交直线MN于点C;
④连结AC,BC.
所以,△ABC即为所求作的等腰直角三角形.
请根据小美的作法,用直尺和圆规作以AB为底的等腰直角三角形ABC,并保留作图痕迹.这种作法的依据是 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com