练习册

  • 练习册
  • 试题
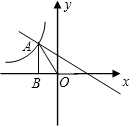
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图，已知Rt△AOB的顶点A是一次函数y=-x+m+3的图象与反比例函数y=
    mx
    的图象在第二象限的交点，且S△AOB=1，则点A的坐标为
     
    ．
    分析：设出点A的坐标，利用所给的面积求得反比例函数解析式，进而求得一次函数解析式，让两个函数解析式组成方程组求解即可．
    解答：精英家教网解：设A（x，y），
    ∵S△AOB=1，
    ∴
    1
    2
    ×（-x）y=1，xy=-2，
    ∵A在反比例函数解析式上，
    ∴m=xy=-2，
    由题意得
    y=-x+1
    y=-
    2
    x
    ，
    解得：x=2，y=-1，或x=-1，y=2，
    ∵图象在第二象限，
    ∴A（-1，2）．
    故答案为：（-1，2）．
    点评：本题考查了反比例函数与一次函数的交点，难度不大，掌握利用所给的三角形的面积先算出反比例函数的关系式，过某个点，这个点的坐标应适合这个函数解析式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知Rt△ABC外切于⊙O，E、F、H为切点，∠ABC=90°，直线FE、CB相交于D点，连接AO、HE、HF，则下列结论：①∠EFH=45°；②∠FEH=45°+∠FAO；③BD=AF；④DH2=AO•DF．其中正确结论的个数为（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2011•辽阳）如图，已知Rt△ABO，∠BAO=90°，以点O为坐标原点，OA所在直线为y轴，建立平面直角坐标系，AO=3，∠AOB=30°，将Rt△ABO沿OB翻折后，点A落在第一象限内的点D处．
    （1）求D点坐标；
    （2）若抛物线y=ax2+bx+3（a≠0）经过B、D两点，求此抛物线的表达式；
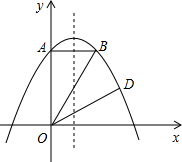    （3）若抛物线的顶点为E，它的对称轴与OB交于点F，点P为射线OB上一动点，过点P作y轴的平行线，交抛物线于点M．是否存在点P，使得以E、F、M、P为顶点的四边形为等腰梯形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
    参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是（-
    b
    2a
    ，
    4ac-b2
    4a
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知Rt△ABO，∠BAO=90°，以点O为坐标原点，OA所在直线为y轴，建立平面直角坐标系，AO=3，∠AOB=30°，将Rt△ABO沿OB翻折后，点A落在第一象限内的点D处．
    （1）求D点坐标；
    （2）若抛物线y=ax2+bx+3（a≠0）经过B、D两点，求此抛物线的表达式；
    （3）若抛物线的顶点为E，它的对称轴与OB交于点F，点P为射线OB上一动点，过点P作y轴的平行线，交抛物线于点M．是否存在点P，使得以E、F、M、P为顶点的四边形为等腰梯形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
    参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是（-数学公式，数学公式）．

    查看答案和解析>>

    科目：初中数学 来源：2011年辽宁省辽阳市中考数学试卷（解析版） 题型：解答题

    如图，已知Rt△ABO，∠BAO=90°，以点O为坐标原点，OA所在直线为y轴，建立平面直角坐标系，AO=3，∠AOB=30°，将Rt△ABO沿OB翻折后，点A落在第一象限内的点D处．
    （1）求D点坐标；
    （2）若抛物线y=ax2+bx+3（a≠0）经过B、D两点，求此抛物线的表达式；
    （3）若抛物线的顶点为E，它的对称轴与OB交于点F，点P为射线OB上一动点，过点P作y轴的平行线，交抛物线于点M．是否存在点P，使得以E、F、M、P为顶点的四边形为等腰梯形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
    参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是（-，）．

    查看答案和解析>>

    科目：初中数学 来源：2009年湖北省武汉市新洲区初中毕业年级数学试卷（解析版） 题型：选择题

    （2009•新洲区模拟）如图，已知Rt△ABC外切于⊙O，E、F、H为切点，∠ABC=90°，直线FE、CB相交于D点，连接AO、HE、HF，则下列结论：①∠EFH=45°；②∠FEH=45°+∠FAO；③BD=AF；④DH2=AO•DF．其中正确结论的个数为（ ）

    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    同步练习册答案