
 某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
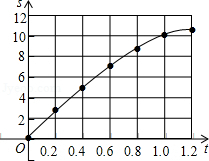 解:(1)描点画图即可;
解:(1)描点画图即可;
|
|
| 4ac-b2 |
| 4a |
| -152 |
| 4×(-5) |
| 45 |
| 4 |
| 45 |
| 4 |


科目:初中数学 来源: 题型:

| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
| s1 |
| t1 |
| s2 |
| t2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较![]() 与
与![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.

查看答案和解析>>
科目:初中数学 来源:2012年浙江省台州市中考数学试卷(解析版) 题型:解答题
| 时间t(秒) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … | |
| 行驶距离s(米) | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
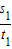 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省仪征市九年级上学期末考试数学试卷(解析版) 题型:解答题
某汽车在刹车后行驶的距离s(单位:m)与时间t(单位:s)之间的关系得部分数据如下表:
|
时间t(s) |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
… |
|
行驶距离s(m) |
0 |
2.8 |
5.2 |
7.2 |
8.8 |
10 |
10.8 |
… |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;

(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)刹车后汽车行驶了多长距离才停止?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com