
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则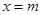 时,
时, 的最大值为
的最大值为 .
.

请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.
(1)y="49" (2)y="2p2+4p+1" 或17 (3)t=1或t=-5.
【解析】
试题分析:(1) ∵y=2x2+4x+1∴y=2(x+1)2-1.
∴对称轴x="-1,又-2≤x≤4时,y的最大值,当x=4时,y有最大值为49.(2)∵P≤x≤2" 由于二次函数具有对称性,当x=2与x=-4时,函数值相等,而x=-1时,y有最小值,是因为a﹥0,图像开口向上。∴当p≤-4,x=p时,y有最大值,y=2p2+4P+1.当-4﹤p≤2,x="2时,y有最大值" y="17.(3)当t≥-1,x=t+2时,y有最大值,即2(t+2" )2+4(t+2)+1=31 (t+7)(t-1)="0"
∴t1="1" t2="-7(舍去)" 当t﹤-1,x=t时,y有最大值,即2t2+4t+1="0"
(t+5)(t-3)="0" t1="-5" t2=3(舍去)。∴t=1或t=-5解:(1)当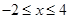 时,二次函数
时,二次函数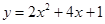 的最大值为 49 ; …… 1分
的最大值为 49 ; …… 1分
(2)∵二次函数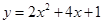 的对称轴为直线
的对称轴为直线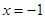 ,
,
∴由对称性可知,当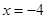 和
和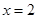 时函数值相等.
时函数值相等.
∴若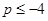 ,则当
,则当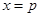 时,
时,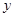 的最大值为
的最大值为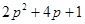 .
.................... 2分
.
.................... 2分
若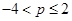 ,则当
,则当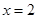 时,
时,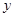 的最大值为17.
............................. 3分
的最大值为17.
............................. 3分
(3)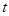 的值为
的值为 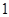 或
或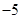 . .................................................. 5分
. .................................................. 5分
阅卷说明:只写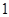 或只写
或只写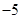 得1分;有错解得0分.
得1分;有错解得0分.
考点:二次函数的图像与性质,即对称轴,顶点坐标解析式的求法。
点评:本题是难题,难点在于当自变量x的取值范围内要考虑到对称轴的关系,需要讨论。此题还可以依据函数的单调性来讨论,即是在对称轴为准,自变量x在那个范围上是y随着x的增大而增大,即为增函数,反之,减函数。由此得到函数的最值。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:阅读理解
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2013届北京市西城区(北区)九年级上学期期末考试数学试卷(带解析) 题型:解答题
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对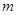 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则 时,
时, 的最大值为
的最大值为 .
.
请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省九年级上学期期末质量抽测数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果 ,求
,求 的值.
的值.

他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为???? ,CG和EH的数量关系为???? , 的值为???? .
的值为???? .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为???? (用含a的代数式表示).
的值为???? (用含a的代数式表示).

(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为???? (用含m,n的代数式表示).
的值为???? (用含m,n的代数式表示).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京海淀区九年级第一学期期中测评数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明在研究中心对称问题时发现:
如图1,当点 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 旋转180°得到
旋转180°得到 点,这时点
点,这时点 与点
与点 重合.
重合.
如图2,当点 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.



(1)请在图2中画出点 、
、 ,
小明在证明P、
,
小明在证明P、 两点关于点
两点关于点 中心对称时,除了说明P、
中心对称时,除了说明P、 、
、 三点共线之外,还需证明;
三点共线之外,还需证明;
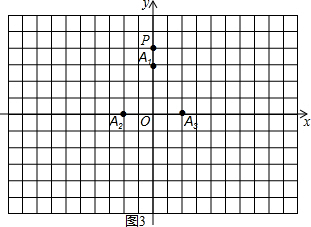
(2)如图3,在平面直角坐标系xOy中,当 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐标为(),点
的坐标为(),点 的坐为.
的坐为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com