
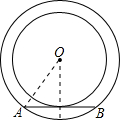
 如图,两个同心圆的半径分别为8cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为
如图,两个同心圆的半径分别为8cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:

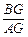 的值.
的值.查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷数学卷 题型:解答题
(本小题满分12分)如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.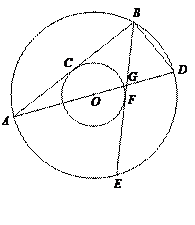
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求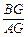 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2008年安徽省芜湖市安师大附中科技特长班招生考试数学试卷(解析版) 题型:填空题
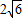 和
和 ,矩形ABCD边AB,CD分别为两圆的弦,当矩形ABCD面积取最大值时,矩形ABCD的周长是 .
,矩形ABCD边AB,CD分别为两圆的弦,当矩形ABCD面积取最大值时,矩形ABCD的周长是 .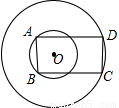
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com