
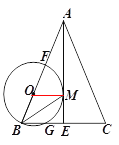
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的位置如图所示,且|a|<|b|,下列各式中正确的个数是( )
①a+b<0;②b﹣a>0;③![]() ;④3a﹣b>0;⑤﹣a﹣b>0.
;④3a﹣b>0;⑤﹣a﹣b>0.
![]()
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①全等三角形的对应边上的中线,高线,对应角的平分线对应相等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;③两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;④两边和其中一边上的高线(或第三边上的高线)对应相等的两个三角形全等.其中正确命题有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L1:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线L2都经过y轴上的一点P,且抛物线L1与顶点Q在直线L2上,则称此直线L2与该抛物线L1具有“一带一路”关系,此时,直线L2叫做抛物线L1的“带线”,抛物线L1叫做直L2的“路线”.
(1) 若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,则m+n=_______.
(2) 若某“路线”L1的顶点在反比例函数![]() 的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
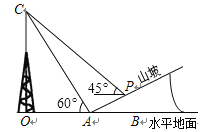
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为![]() (即tan∠PAB=
(即tan∠PAB=![]() ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.

问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
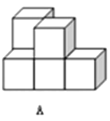
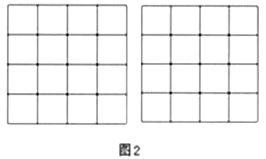
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体![]() ,如图所示.
,如图所示.
(1)请画出这个几何体![]() 的三视图.
的三视图.
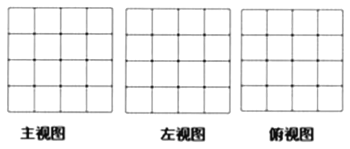
(2)若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
(4)若另一个几何体![]() 与几何体
与几何体![]() 的主视图和左视图相同,而小正方体个数则比几何体
的主视图和左视图相同,而小正方体个数则比几何体![]() 多1个,请在图2中画出几何体
多1个,请在图2中画出几何体![]() 的俯视图中的任意两种.
的俯视图中的任意两种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
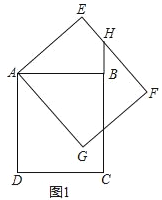
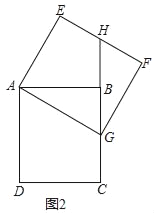
(1)求证:BH=EH;
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读理解]射线![]() 是
是![]() 内部的一条射线,若
内部的一条射线,若![]() 则我们称射线
则我们称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
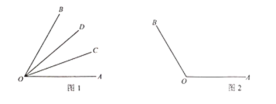
例如,如图1,![]() ,则
,则![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线:同时,由于
的伴随线:同时,由于![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
[知识运用]
(1)如图2,![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,则
的伴随线,则![]() ,若
,若![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,则
的平分线,则![]() 的度数是 .(用含
的度数是 .(用含![]() 的代数式表示)
的代数式表示)
(2)如图,如![]() ,射线
,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,射线
的速度逆时针旋转,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线![]() 与射线
与射线![]() 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.

①是否存在某个时刻![]() (秒),使得
(秒),使得![]() 的度数是
的度数是![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②当![]() 为多少秒时,射线
为多少秒时,射线![]() 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com