
 OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
 ,∴△AOD≌△COE(ASA)。
,∴△AOD≌△COE(ASA)。 OA。
OA。 ,即OP•OC=OE2。
,即OP•OC=OE2。

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

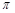 取3.14)。
取3.14)。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
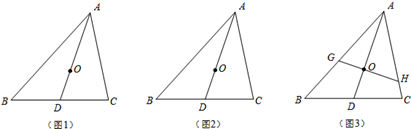
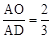 ;
;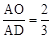 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;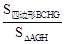 的最大值.
的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= ,则ΔCEF的周长等于
,则ΔCEF的周长等于
| A.8 | B.9.5 | C.10 | D.11.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com