
【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 . 
【答案】![]()
【解析】解:连接AF,如图所示: 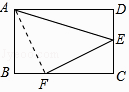
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵FC=2BF,
∴BF=1,FC=2,
∴AB=FC,
∵E是CD的中点,
∴CE= ![]() CD=1,
CD=1,
∴BF=CE,
在△ABF和△FCE中, 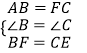 ,
,
∴△ABF≌△FCE(SAS),
∴∠BAF=∠CFE,AF=FE,
∵∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°﹣90°=90°,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴ocs∠AEF= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】掌握矩形的性质和解直角三角形是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD=CD,∠ABD=∠ACD=90°,点E、F分别在AB、AC上,若ED平分∠BEF.
(1)求证:FD平分∠EFC.
(2)若EF=4,AF=6,AE=5,求BE和CF的和的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
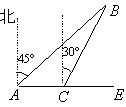
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度![]() 当点M第一次到达B点时,M、N同时停止运动.
当点M第一次到达B点时,M、N同时停止运动.![]() 点M、N运动几秒后,M、N两点重合?
点M、N运动几秒后,M、N两点重合?![]() 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形![]() ?
?![]() 当点M、N在BC边上运动时,能否得到以MN为底边的等腰
当点M、N在BC边上运动时,能否得到以MN为底边的等腰![]() ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】”切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时﹣﹣1.5小时;C:1.5小时﹣﹣2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图, 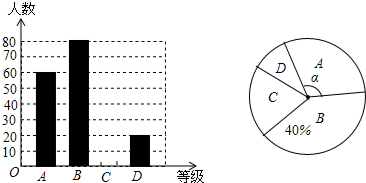
请根据图中信息解答下列问题:
(1)该校共调查了学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角α的度数是;
(4)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)判断直线BE与抛物线交点的个数;
(3)求证:CD垂直平分BE;
(4)若P是该抛物线上的一个动点,是否存在这样的点P,使得△PBE是等腰直角三角形,且∠PEB=90°?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com