
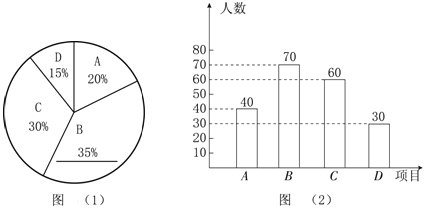
【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共调查了________名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率.
【答案】(1)200;(2)答案见解析;(3)![]() .
.
【解析】试题分析:根据A组的人数和百分比求出总人数,然后分别求出C组的人数和B组的百分比,完成统计图;根据题意列出表格,求出概率.
试题解析:(1)40÷20%=200(名)
(2)C组人数:200-40-70-30=60(名) B组百分比:70÷200×100%=35% 如图
(3)用![]() 表示喜欢跳绳的学生,用B表示喜欢足球的学生,列表如下
表示喜欢跳绳的学生,用B表示喜欢足球的学生,列表如下
第一人 | C1 | C2 | C3 | B |
C1 | (C2,C1) | (C3,C1) | (B, C1) | |
C2 | (C1,C2) | (C3,C2) | (B, C2) | |
C3 | (C1,C3) | (C2,C3) | (B, C3) | |
B | (C1,B) | (C2,B) | (C3,B) |
∴P(一人是喜欢跳绳,一人是喜欢足球的学生)=![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
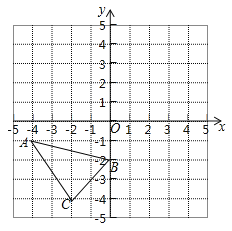
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 从原点
从原点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向右平移,直线
轴向右平移,直线![]() 分别交直线
分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,以
,以![]() 为边向左侧作正方形
为边向左侧作正方形![]() ,当直线
,当直线![]() 经过点
经过点![]() 时停止运动,设直线
时停止运动,设直线![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
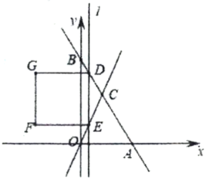
(1)![]() ________,
________,![]() ________;
________;
(2)设线段![]() 的长度为
的长度为![]() (
(![]() );求
);求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当正方形![]() 的边
的边![]() 落在
落在![]() 轴上时,求出
轴上时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米;④甲、乙两名运动员相距5千米时,t=0.5或t=2或t=5.其中正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一个计算程序;

(1)若输入的x=3,则输出的结果为 ;
(2)若开始输入的x为正整数,最后输出的结果为40,则满足条件的x的不同值最多有 ;
(3)规定:程序运行到“判断结果是否大于30”为一次运算.若运算进行了三次才输出,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com