
【题目】如图,在平面直角坐标系中,![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标为
的坐标为![]() ,请解答下列问题:
,请解答下列问题:
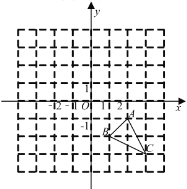
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,点
,点![]() 的坐标为______;
的坐标为______;
(2)在网格内以点![]() 为位似中心,把
为位似中心,把![]() 按相似比
按相似比![]() 放大,得到
放大,得到![]() ,请画出
,请画出![]() ;若边
;若边![]() 上任意一点
上任意一点![]() 的坐标为
的坐标为![]() ,则两次变换后对应点
,则两次变换后对应点![]() 的坐标为______.
的坐标为______.
【答案】(1)图见解析,(2,1);(2)图见解析,![]()
【解析】
(1)依次作出点A、B、C三点关于x轴的对称点A1、B1、C1,再顺次连接即可;根据关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数写出即可;
(2)根据位似图形的性质作图即可;先求出经过一次变换(关于x轴对称)的点的坐标,再根据关于(1,1)为位似中心的点的坐标规律:横坐标=-2×(原横坐标-1)+1,纵坐标=-2×(原纵坐标-1)+1,代入化简即可.
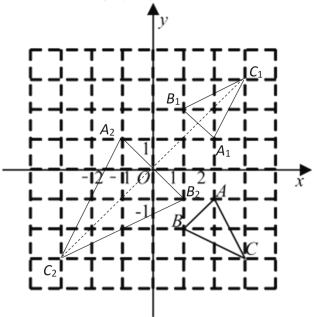
解:(1)![]() 如图所示,点
如图所示,点![]() 的坐标为(2,1);
的坐标为(2,1);
(2)![]() 如图所示,点
如图所示,点![]() 的坐标为
的坐标为![]() ,则其关于x轴对称的点的坐标是(m,-n),关于点
,则其关于x轴对称的点的坐标是(m,-n),关于点![]() 位似后的坐标为(
位似后的坐标为(![]() ,
,![]() ),即两次变换后对应点
),即两次变换后对应点![]() 的坐标为:
的坐标为:![]() .
.
故答案为:![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长都是1的小正方形组成的网格中,P,Q,B,C均为格点,线段PQ、BC相交于点A.
(Ⅰ)PA:AQ= ;
(Ⅱ)尺规作图:设∠QAB=α,将线段AB绕点A逆时针旋转α+90°的角,点B的对应点为B′,请你画出点B′.

查看答案和解析>>
科目:初中数学 来源: 题型:
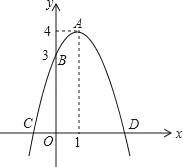
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
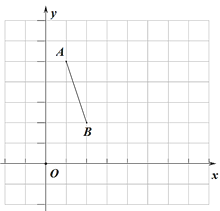
【题目】如图,在平面直角坐标系中有点A(1,5),B(2,2),将线段AB绕P点逆时针旋转90°得到线段CD,A和C对应,B和D对应.
(1)若P为AB中点,画出线段CD,保留作图痕迹;
(2)若D(6,2),则P点的坐标为 ,C点坐标为 .
(3)若C为直线![]() 上的动点,则P点横、纵坐标之间的关系为 .
上的动点,则P点横、纵坐标之间的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为![]() 个单位的正方形,在建立平面直角坐标系后,
个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

![]() 以点
以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 放大得到
放大得到![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,在网格中画出图形,并直接写出点
倍,在网格中画出图形,并直接写出点![]() 所对应的点
所对应的点![]() 的坐标.
的坐标.
![]() 在网格中,画出
在网格中,画出![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 的
的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.

(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com