
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 将
将![]() 沿
沿![]() 轴折叠,使点
轴折叠,使点![]() 落在
落在![]() 轴的点
轴的点![]() 上,设
上,设![]() 为线段
为线段![]() 上的一个动点,点
上的一个动点,点![]() 与点
与点![]() 不重合,连接
不重合,连接![]() .以点
.以点![]() 为端点作射线
为端点作射线![]() 交线段
交线段![]() 于点
于点![]() 使
使![]() .
.
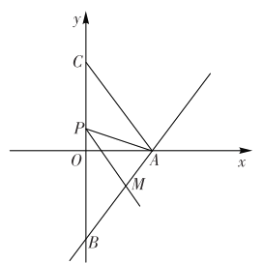
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 当
当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
![]() 是否存在点
是否存在点![]() 使
使![]() 为直角三角形?若存在,请直接写出点
为直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)先利用待定系数法求得函数关系式,进而求得点B坐标,再利用对称性求得C的坐标即可;
(2)先利用轴对称性及三角形的外角性质证得![]() ,再根据勾股定理求得AC长,利用“ASA”可证得
,再根据勾股定理求得AC长,利用“ASA”可证得![]() ,进而可求得BM,AM的长,过点
,进而可求得BM,AM的长,过点![]() 作
作![]() 轴于点
轴于点![]() ,由此可得
,由此可得![]() ,利用相似三角形的性质可求得点M的坐标,最后利用待定系数法即可求得直线CM的函数关系式;
,利用相似三角形的性质可求得点M的坐标,最后利用待定系数法即可求得直线CM的函数关系式;
(3)分类讨论,当![]() 时,则有
时,则有![]() ,利用相似三角形的性质可求得点
,利用相似三角形的性质可求得点![]() 的坐标,当
的坐标,当![]() 时,则
时,则![]() ,进而可证得
,进而可证得![]() ,再根据过点
,再根据过点![]() 只有一条直线与
只有一条直线与![]() 垂直,即可求得此时的点
垂直,即可求得此时的点![]() 的坐标为
的坐标为![]()
解:(1)∵直线![]() 与
与![]() 轴相交于点
轴相交于点![]()
∴![]()
![]()
![]() 直线的解析式为
直线的解析式为![]()
令![]() 则
则![]()
![]()
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]()
(2)∵点![]() 与点
与点![]() 关于
关于![]() 轴对称
轴对称
![]()
![]()
![]()
![]()
![]()
![]()
在△PAC与△MPB中,
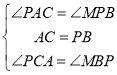
![]() (ASA)
(ASA)
![]()
![]()
过点![]() 作
作![]() 轴于点
轴于点![]() .
.
![]()
![]()
![]() ,
,![]()
![]()
![]() 点
点![]() 的坐标是
的坐标是![]()
又点![]() 的坐标为
的坐标为![]()
设直线CM为![]() ,
,
则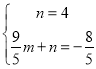 ,
,
解得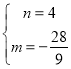
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(3)存在,![]() ,
,![]()
由题意,得![]()
当![]() 时,则有
时,则有![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
当![]() 时,则
时,则![]()
![]()
![]()
![]()
![]()
![]() 过点
过点![]() 只有一条直线与
只有一条直线与![]() 垂直,
垂直,
![]() 此时点
此时点![]() 与点
与点![]() 重合,即符合条件的点
重合,即符合条件的点![]() 的坐标为
的坐标为![]()
![]() 使
使![]() 为直角三角形的点
为直角三角形的点![]() 有两个,
有两个,![]() ,
,![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
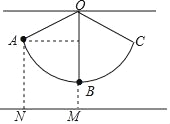
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
【答案】15cm
【解析】
试题设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
试题解析:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
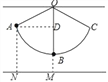
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14﹣5=9cm,
∴OD=x﹣9,
在Rt△AOD中,cos∠AOD=![]() ,
,
∴cos66°=![]() =0.40,
=0.40,
解得:x=15,
∴OB=15cm.
【题型】解答题
【结束】
20
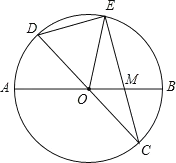
【题目】已知:如图,在半径为![]() 的
的![]() 中,
中,![]() 、
、![]() 是两条直径,
是两条直径,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() 。
。![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在五十天内试销一款成本为40元/间的新型商品,此款商品在第![]() 天的销售量
天的销售量![]() (件)与销售的天数
(件)与销售的天数![]() 的关系为
的关系为![]() ,销售单价
,销售单价![]() (元/件)与
(元/件)与![]() 满足:当
满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求该超市销售这款商品第![]() 天获得的利润
天获得的利润![]() (元)关于
(元)关于![]() 的函数关系式;
的函数关系式;
(2)这五十天,该超市第几天获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿ABC中,∠CBA=90,∠CAB=50,以AB为直径作⊙O交AC于点D,点E在边BC上,连结DE,且∠DEB=80
(1)求证:直线ED是⊙O的切线;
(2)求证:DE=BE

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com