
 ,设AB=x,AD=y。
,设AB=x,AD=y。
 (2)2(3)
(2)2(3)

 。
。 ,
, ,即
,即 。
。 。
。 。
。 。
。 。
。
 AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,
 。
。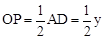 ,设PF=t,则
,设PF=t,则 ,即
,即 。
。 ,则
,则 ,
, (负值舍去)。
(负值舍去)。 时,
时, 最小,最小值为2。
最小,最小值为2。 的最小值为
的最小值为 。
。 列式得到y与x的函数关系式。
列式得到y与x的函数关系式。 AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得 ,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。
,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
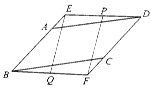
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.11+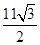 | B.11﹣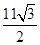 |
C.11+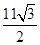 或11﹣ 或11﹣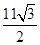 | D.11+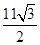 或1+ 或1+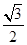 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

 时,四边形A′CDF为正方形
时,四边形A′CDF为正方形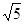 时,四边形BA′CD为等腰梯形;
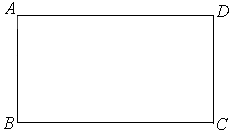
时,四边形BA′CD为等腰梯形;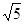 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com