Question

如图，已知A(0，1)、C(4，3)、E，P是以AC为对角线的矩形ABCD内部(不在各边上)的一个动点，点D在y轴，抛物线y＝ax²＋bx＋1以P为顶点．

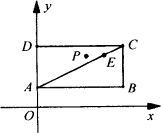
(1)说明点A、C、E在一条直线上；

(2)能否判断抛物线y＝ax²＋bx＋1的开口方向？请说明理由；

(3)设抛物线y＝ax²＋bx＋1与x轴有交点F、G(F在G的左侧)，△GAO与△FAO的面积差为3，且这条抛物线与线段AE有两个不同的交点．这时能确定a、b的值吗？若能，请求出a、b的值；若不能，请确定a、b的取值范围．

Answer 1

答案：
解析：

解： 　　(1)如图，由题意，A(0，1)、C(4，3)确定的解析式为：y＝x＋1．将点E的坐标E代入y＝x＋1中，左边＝，右边＝×＋1＝， 　　∵左边＝右边，∴点E在直线y＝x＋1上，即点A、C、E在一条直线上． 　　(2)解法一：能．由于动点P在矩形ABCD内部，∴点P的纵坐标大于点A的纵坐标，而点A与点P都在抛物线上，且P为顶点，∴这条抛物线有最高点，抛物线的开口向下． 　　解法二：能．∵抛物线y＝ax2＋bx＋c的顶点P的纵坐标为，且P在矩形ABCD内部， 　　∴1＜＜3，由1＜1－得＞0，∴a＜0，∴抛物线的开口向下． 　　(3)不能，只能确定a、b的取值范围． 　　连接GA、FA，∵S△GAF－S△FAO＝3 　　∴GO·AO－FO·AO＝3 　　∴OA＝1， 　　∴GO－FO＝6． 　　设F(x1，0)、G(x2，0)，则x1、x2为方程ax2＋bx＋c＝0的两个根，且x1＜x2， 　　又∵a＜0，∴x1·x2＝＜0，∴x1＜0＜x2， 　　∴GO＝x2，FO＝－x1，∴x2－(－x1)＝6，即x2＋x1＝6，∵x2＋x1＝，∴＝6， 　　∴b＝－6a，∴抛物线解析式为：y＝ax2－6ax＋1，其顶点P的坐标为(3，1－9a)， 　　由方程组得ax2－(6a＋)x＝0 　　∵顶点P在矩形ABCD内部，∴1＜1－9a＜3，∴＜a＜0． 　　∴x＝0或x＝＝6＋． 　　当x＝0时，即抛物线与线段AE交于点A，而这条抛物线与线段AE有两个不同的交点，则有0＜6＋≤，解得≤a＜ 　　综合得＜a＜．∵b＝－6a，∴＜b＜．