
����Ŀ������̽��
������ͼ�ΰ���ij�ַ�������任����һ�ּ���ͼ�εĹ��̽������α任����ת�任�Ǽ��α任��һ�ֻ���ģ�ͣ�������ת��������ʹͼ�εļ��������������֣�����ͽ����е�Ԫ���ɷ�ɢ��Ϊ���У��֮��Ĺ�ϵ������ˣ��Ӷ�������������ת����
�����������ͼ1��![]() �DZ߳�Ϊ1�ĵȱ������Σ�
�DZ߳�Ϊ1�ĵȱ������Σ�![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ����
����![]() ����Сֵ��
����Сֵ��
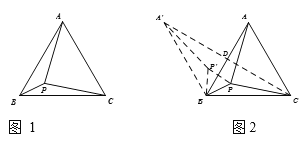
����ͨ��ת����������������һ�㷢���������߶�(������)ת��Ϊ������֮�������(����Ϊ��)��������������֮���߶����������Сֵ(����Ϊֱ)��
����������ͼ2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֪
����֪![]() ��
��![]() ����
����![]() ��
��![]() ����֪
����֪![]() Ϊ�������Σ���
����������![]() ��
��
��![]() ����ˣ���
����ˣ���![]() ����ʱ��
����ʱ��![]() ����Сֵ��
����Сֵ��![]() ��
��
ѧ�����ã�(1)��ͼ3����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��__________��
����Сֵ��__________��
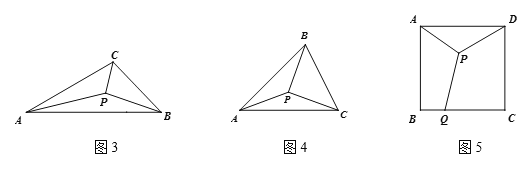
(2)��ͼ4����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��
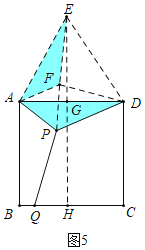
(3)��ͼ5��![]() �DZ߳�Ϊ2��������
�DZ߳�Ϊ2��������![]() ��һ�㣬
��һ�㣬![]() Ϊ��
Ϊ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��
���𰸡���1��5����2��![]() ����3��
����3��![]() .
.
��������
��1����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����֪
����֪![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����֪
����֪![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��3����ͼ5�У���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������֪
������֪![]() �ǵȱ������Σ�ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á����߶���̡�����Сֵ��
�ǵȱ������Σ�ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á����߶���̡�����Сֵ��
�⣺��1����ͼ3�У�
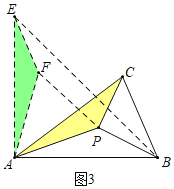
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ��
��
��![]() ��
��![]() ����CAE=PAF=60����
����CAE=PAF=60����
��AE=AC=3��AF=AP��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
�ߡ�BAC=30�㣬
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ����СֵΪ5��
����СֵΪ5��
�ʴ�Ϊ5��
��2����ͼ4�У�
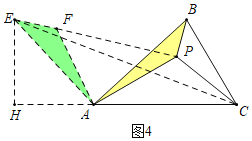
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ��
��
��AF=AP����FAP=90�㣬
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��FP=![]() ��
��
�ߡ�BAC=45�㣬
��![]() ��
��![]() ��
��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��
��![]() ��
�У�
![]() ��
��![]() ��
��![]()
![]() ��
��
��![]() ��
�У�![]()
![]()
![]() ��
��
![]() ��
��
![]() ����СֵΪ
����СֵΪ![]() ��
��
��3����ͼ5�У���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������֪
������֪![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
��֪![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ����СֵΪ
����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����������
3��9��27��81����
1��3��9��27����
2��10��26��82����
(1)�ڢ�������ʲô��������?
(2)�ڢڢ�������ڢ������ֱ���ʲô��ϵ?
(3)��x,y,z�ֱ�Ϊ�ڢ٢ڢ� �е�2019��������![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ij����ʻ�����У������е�ʣ������y����������ʻ·��x��ǧ�ף�֮����һ�κ�����ϵ���䲿��ͼ����ͼ��ʾ��
��1����y����x�ĺ�����ϵʽ��������Ҫд������
��2����֪�������е�ʣ������Ϊ8��ʱ���������Ὺʼ��ʾ���ͣ��ڴ˴���ʻ�����У���ʻ��500ǧ��ʱ��˾��������ǰ������ļ���վ��30ǧ��·�̣��ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·���Ƕ���ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=AD��AB��BC��AD��CD��P�ǶԽ���AC��һ�㣬

��֤��PB=PD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��618���д�ٻ�У�������̷��ڽ��н��۴�����ij��������������A���װ���м۸�����������۱�ƽʱ�ۼ�ÿ����90Ԫ�����������ͬ������A���װ��ƽʱ���۶�Ϊ5��Ԫ�����������۶�ֻ��4��Ԫ��
(1)�õ���A���װƽʱÿ���ۼ�Ϊ����Ԫ?
(2)�õ�����6��1��6��2��һ�ִ����У�A���װ����������dz��𱬣��̼Ҿ���Ϊ�ڶ���6��16��6��18����ٽ�һ����������A���ͬʱ�ٹ���ͬƷ�Ƶ�B���װ����֪A���װÿ������Ϊ300Ԫ��B���װÿ������Ϊ200Ԫ������Ԥ���ò�����7.2��Ԫ�Ҳ�����7.3��Ԫ���ʽ��������װ��300����������һ�㣬�̼ҹ��м��ֽ�������?
(3)��6��16��6��18������У�A������ƽ�ռ۽�90Ԫ������B���װÿ���ۼ�Ϊ280Ԫ��Ϊ��B���װ����·�����̾���ÿ�۳�һ��B���װ�������˿��ֽ�![]() Ԫ��Ҫʹ(2)����������װȫ����������з���������ͬ��
Ԫ��Ҫʹ(2)����������װȫ����������з���������ͬ��![]() ��ֵӦ�Ƕ���?
��ֵӦ�Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ�����ͼ���㣨3��2���ͣ�1��4����
��1�������˺�����ͼ��
��2�����һ�κ����ı���ʽ��
��3�����˺�����ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B�����߶�AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
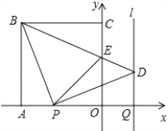
����Ŀ����ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ����4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s����
��1����PBD�Ķ���Ϊ ����D������Ϊ ����t��ʾ����
��2����tΪ��ֵʱ����PBEΪ���������Σ�
��3��̽����POE�ܳ��Ƿ���ʱ��t�ı仯���仯�����仯��˵�����ɣ������䣬���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ�� 2��0 ������4��0������C������Ϊ��m�� ![]() m����mΪ�Ǹ���������CA+CB����Сֵ��_____��
m����mΪ�Ǹ���������CA+CB����Сֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
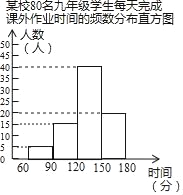
����Ŀ��Ϊ�˽���꼶��ҵ���������ijУ�����ȡ80�����꼶ѧ�������ʾ����飬��������������80����Ч�ʾ�������ʱ���֣�ÿ����ɿ�����ҵʱ�䣬�������180���ӣ���̲�����60���ӣ��������������Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ��
��1���������80��ѧ��ÿ����ɿ�����ҵʱ�����λ����_____�飨��ʱ�䷶Χ����
��2����У���꼶����800��ѧ�������ƴ�Լ��_____��ѧ��ÿ����ɿ�����ҵʱ����120�������ϣ�����120���ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com