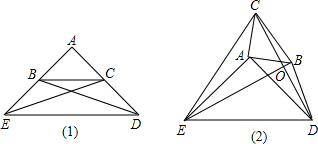
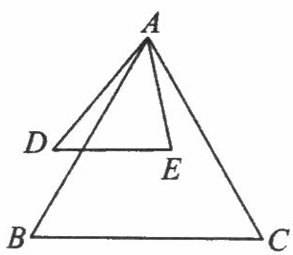
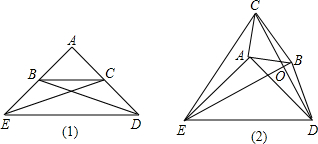
解:(1)AB=AC.
理由如下:∵EC、DB分别平分∠AED、∠ADE,
∴∠AEC=

∠AED,∠ADB=

∠ADE,
∵∠AED=∠ADE,
∴∠AEC=∠ADB,
在△AEC和△ADB中,
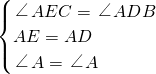
,
∴△AEC≌△ADB(ASA),
∴AB=AC;
(2)BE=CD且BE⊥CD.
理由如下:∵∠EAD=∠BAC,
∴∠EAD+∠BAD=∠BAC+∠BAD,
即∠EAB=∠DAC,
在△AEB和△ADC中,
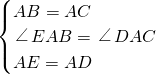
,
∴△AEB≌△ADC(SAS),
∴EB=CD,
∴∠AEB=∠ADC,
∵∠AEB+∠DEB+∠ADE=90°,
∴∠ADC+∠DEB+∠ADE=90°,
∵∠ADC+∠DEB+∠ADE+∠DOE=180°,
∴∠DOE=90°,
∴BE⊥CD;
(3)S
四边形CEDB=S
△BCD+S
△CDE=

CD•BO+

CD•EO,
=

CD•(BO+EO),
=

CD•BE,
=

CD
2,
∵CD=8,
∴四边形CEDB的面积=

×8
2=

×64=32.
分析:(1)根据角平分线的定义求出∠AEC=∠ADB,然后利用“角边角”证明△AEC与△ADB全等,根据全等三角形对应边相等即可证明;
(2)先根据∠EAD=∠BAC证明∠EAB=∠DAC,然后利用“边角边”证明△AEB和△ADC全等,再根据全等三角形对应边相等可得BE=CD,全等三角形对应角相等可得∠AEB=∠ADC,然后证明∠ADC+∠DEB+∠ADE=90°,再根据三角形内角和定理可得∠DOE=90°,从而证明BE⊥CD;
(3)把四边形的面积分成△BCD与△CDE两个三角形,然后根据三角形的面积公式列式整理为四边形的面积等于

CD
2,再代入数据进行计算即可得解.
点评:本题考查了全等三角形的判定与性质,角平分线的定义,以及旋转变换的性质,准确识图,找出三角形全等的条件是解题的关键.

 ∠AED,∠ADB=
∠AED,∠ADB= ∠ADE,
∠ADE,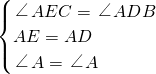 ,
,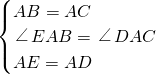 ,
, CD•BO+
CD•BO+ CD•EO,
CD•EO, CD•(BO+EO),
CD•(BO+EO), CD•BE,
CD•BE, CD2,
CD2, ×82=
×82= ×64=32.
×64=32. CD2,再代入数据进行计算即可得解.
CD2,再代入数据进行计算即可得解.