
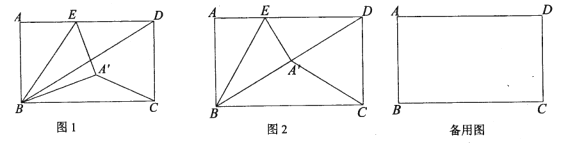
【题目】如图,在矩形![]() 中,
中,![]() ,点E是
,点E是![]() 边上的动点,将矩形
边上的动点,将矩形![]() 沿
沿![]() 折叠,点A落在点
折叠,点A落在点![]() 处,连接
处,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,若点![]() 恰好落在
恰好落在![]() 上,求
上,求![]() 的值;
的值;
(3)点E在![]() 边上运动的过程中,
边上运动的过程中,![]() 的度数是否存在最大值,若存在,求出此时线段
的度数是否存在最大值,若存在,求出此时线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析,(2)![]() =
=![]() ,(3)
,(3)![]() 的度数是最大值为90°,此时线段
的度数是最大值为90°,此时线段![]() 的长=
的长=![]() .
.
【解析】
![]() 由折叠知∠AEB=∠A’EB,再利矩形性质可得
由折叠知∠AEB=∠A’EB,再利矩形性质可得![]() ,结合直角三角形两锐角互余即可得出结论;
,结合直角三角形两锐角互余即可得出结论;![]() 先由矩形性质结合勾股定理求得
先由矩形性质结合勾股定理求得![]() ,由折叠性质用勾股定理建立方程求解即可求出AE的长,进而求出结论;
,由折叠性质用勾股定理建立方程求解即可求出AE的长,进而求出结论;![]() 先判断出∠A’CB最大时,点
先判断出∠A’CB最大时,点![]() 在CE上,进而利用三角形的面积求出CE,进而用勾股定理求出DE,即可得出结论.
在CE上,进而利用三角形的面积求出CE,进而用勾股定理求出DE,即可得出结论.
解:![]() 由折叠知∠AEB=∠A’EB,
由折叠知∠AEB=∠A’EB,
∴∠AEB=![]() =
=![]() ,
,![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =2∠ABE;
=2∠ABE;![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
设![]() ,
,![]() ,
,
由折叠知,![]() ,
,![]() ,
,![]() ,
,![]() =BD-
=BD-![]() =4,
=4,
∴∠DA’E=90°,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() =16,
=16,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ;
;![]() 的度数是存在最大值,
的度数是存在最大值,
理由:如图1,过点B作![]() 交
交![]() 的延长线于F,
的延长线于F,
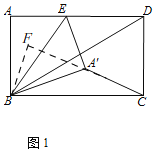
在![]() 中,
中,![]() ,
,![]() 越大时,
越大时,![]() 越大,即
越大,即![]() 越大,
越大,
当点E在边AD上运动时,点![]() 与F重合时,BF最大=A’B=AB=6,
与F重合时,BF最大=A’B=AB=6,
∴A’B⊥A’C,
∴![]() ,
,
由折叠知,![]() ,
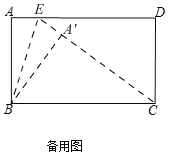
,![]() 点
点![]() 在CE上,如备用图,
在CE上,如备用图,
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]() ,
,
根据三角形面积得:![]() =
=![]() ,
,
∴A’B=AB,![]() ,
,
在![]() 中,根据勾股定理
中,根据勾股定理![]() ,
,![]() .
.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .有一宽度为1,长度足够长的矩形(阴影部分)沿
.有一宽度为1,长度足够长的矩形(阴影部分)沿![]() 轴方向平移,与
轴方向平移,与![]() 轴平行的一组对边交抛物线于点
轴平行的一组对边交抛物线于点![]() 和点
和点![]() ,交直线
,交直线![]() 于点
于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() 和点
和点![]() .
.
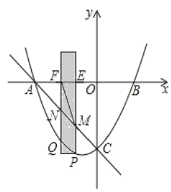
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)当点![]() 和
和![]() 都在线段
都在线段![]() 上时,连接
上时,连接![]() ,如果
,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在矩形的平移过程中,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某特产专卖店销售一种蜜枣,每千克的进价为10元,销售过程中发现,每天销量![]() 与销售单价x(元)之间关系可以近似地看作一次函数
与销售单价x(元)之间关系可以近似地看作一次函数![]() .(利润=售价-进价)
.(利润=售价-进价)
(1)写出每天的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种蜜枣每天能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种蜜枣的销售单价不得高于30元.若商店想要这种蜜枣每天获得300元的利润,则销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
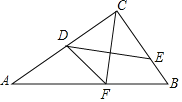
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别在AC、BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处,若AC=12,AB=13,则CD的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月25日是第二十四个“全国中小学生安全教育日”,某校为加强学生的安全意识,以“防火、防溺水、防食物中毒、防校园欺凌”为主题组织了全校学生参加安全知识竞赛,从中抽取了部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,如图所示.
(1)学校共抽取了______名学生,![]() _____,n=______.
_____,n=______.
(2)补全频数直方图;
(3)该校共有2000名学生。若成绩在70分以下(含70分)的学生安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,顶点为
,顶点为![]() .
.

(1)求这条抛物线表达式;
(2)将该抛物线向右平移,平移后的新抛物线顶点为![]() ,它与
,它与![]() 轴交点为
轴交点为![]() ,联结
,联结![]() 、
、![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的正切值;
的正切值;
(3)联结![]() ,在(2)的条件下,射线
,在(2)的条件下,射线![]() 平分
平分![]() ,求点
,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘老师在一节习题课上出示了下面一张幻灯片
解分式方程的基本思想是“____________”,把分式方程变为整式方程求解.解分式方程一定注意要__________.
小明同学的作业如下:![]()
解:去分母得,![]() (第一部)
(第一部)
移项,合并同类项得 ![]() (第二步)
(第二步)
经检验![]() 时,
时,![]() (第三步)
(第三步)
所以原分式方程的解为![]() (第四步)
(第四步)
解分式方程的基本思想是“____________”,把分式方程变为整式方程求解.解分式方程一定注意要__________.
小明同学的作业如下:![]()
解:去分母得,![]() (第一部)
(第一部)
移项,合并同类项得 ![]() (第二步)
(第二步)
经检验![]() 时,
时,![]() (第三步)
(第三步)
所以原分式方程的解为![]() (第四步)
(第四步)
(1)请将幻灯片中的划线部分填上(温馨提示有2个空呦!)
(2)小明解答过程是从第_______步开始出错的,其错误原因是______________;
(3)请你写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx–1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2–2x–1–t=0(t为实数)在–1<x<4的范围内有实数解,则t的取值范围是

A. t≥–2 B. –2≤t<7
C. –2≤t<2 D. 2<t<7
查看答案和解析>>
科目:初中数学 来源: 题型:
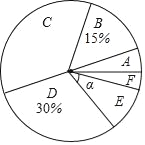
【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com