
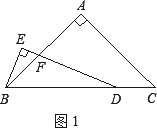
在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
(1)当AB=AC时,(如图1),
①∠EBF=________°;
②探究线段BE与FD的数量关系,并加以证明;
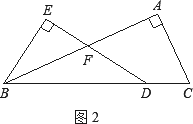
(2)当AB=kAC时(如图2),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
|
分析:(1)①根据题意可判断△ABC为等腰直角三角形,据此即可推断∠C=45°,进而可知∠EDB=22.5°.然后求出∠EBF的度数. ②根据题意证明△BEF∽△DEB,然后利用相似三角形的性质,得到BE与FD的数量关系. (2)作∠ACB的平分线,得到 解答:解:(1)①∵AB=AC∠A=90° ∴∠ABC=∠C=45° ∵∠EDB= ∴∠EDB=22.5° ∵BE⊥DE ∴∠EBD=67.5° ∴∠EBF=67.5°-45°=22.5° ②在△BEF和△DEB中 ∵∠E=∠E=90° ∠EBF=∠EDB=22.5° ∴△BEF∽△DEB 如图:
BG平分∠ABC, ∴BG=GD△BEG是等腰直角三角形 设EF=x,BE=y, 则:BG=GD= FD= ∵△BEF∽△DEB ∴ 即: 得:x=( ∴FD= ∴FD=2BE. (2)如图:
作∠ACB的平分线CG,交AB于点G, ∵AB=kAC ∴设AC=b,AB=kb,BC= 利用角平分线的性质有: 即: 得:AG= ∵∠EDB= ∴tan∠EDB=tan∠ACG= ∵∠EDB= ∠ABC=90°-∠ACB ∴∠EBF=90°-∠ABC-∠EDB= ∴△BEF∽△DEB ∴EF= ED= ∴FD= ∴ 点评:本题考查的是相似三角形的判定与性质,(1)利用等腰直角三角形的性质进行判定和计算.(2)结合图形利用三角函数和相似三角形进行计算求出线段间的关系. |
|
考点:相似三角形的判定与性质;角平分线的性质;等腰直角三角形. |


科目:初中数学 来源:2012年初中毕业升学考试(广西桂林卷)数学(带解析) 题型:解答题
如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B
时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2013届辽宁省大石桥市水源二中九年级上学期阶段检测数学试卷(带解析) 题型:解答题
在△ABC中,AB=AC,∠BAC=α,点D是BC上一动点(不与B、C重合),将线段AD绕点A逆时针旋转α后到达AE位置,连接DE、CE,设∠BCE=β.
(1)如图1,若α=90°,求β的大小;
(2)如图2,当点D在线段BC上运动时,试探究α与β之间的数量关系,并证明你的结论;
(3)当点D在线段BC的反向延长线上运动时(画出图形),(2)中的结论是否仍然成立?若成立,请证明,若不成立,请直接写出α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源:人教版初三年级数学相似形提高测试 题型:填空题
如图,在△ABC中,AB=AC=27,D在AC上,且BD=BC=18,DE∥BC交AB于E,则DE=_______.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省镇江市初一四月月考数学卷 题型:解答题
如图,在ΔABC中,AB=AC=10,BC=8.用尺规作图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com