
【题目】某同学要利用长为24m的篱笆围成一个长方形花圃,形状如图,一边靠墙(墙的最大可用长度为9m),中间隔有一道篱笆,设AB长为x米,围成的花圃面积为S平方米.
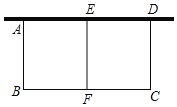
(1)求S关于x的函数解析式;并写出自变量x的取值范围.
(2)当AB多长时,围成的花圃有最大面积?最大面积是多少?
科目:初中数学 来源: 题型:
【题目】某商场以每件![]() 元的价格购进一种商品,试销中发现这种商品每天的销售量
元的价格购进一种商品,试销中发现这种商品每天的销售量![]() (件)与每件的销售价
(件)与每件的销售价![]() (元)满足一次函数关系
(元)满足一次函数关系![]() .
.
(1)求商场销售这种商品每天的销售利润![]() (元)与每件销售价
(元)与每件销售价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到![]() 元?如果能,求出此时的销售价格;如果不能,说明理由.
元?如果能,求出此时的销售价格;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
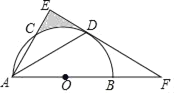
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州苏宁电器某品牌洗衣机销售情况良好,2018年11月份初该洗衣机每台的进价为2280元,购进了600台该品牌洗衣机.
(1)如果该商场为了减小库存压力,想把购进的600台该品牌洗衣机在11月底全部销售完,商场决定利用打折来促销,每台洗衣机在标价的基础上打8折,这样很快销售一空.要使该商场获得利润不低于72000元,则每台洗衣机的标价应不低于多少元?
(2)该商场决定12月初继续购进600台该品牌洗衣机销售,据悉,2018年12月份因全国经济出现通货膨胀,商品价格进一步上涨,商场决定该品牌洗衣机的销售价格比(1)中的最低标价上涨m%,但实际销售量比11月份下降了![]() m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
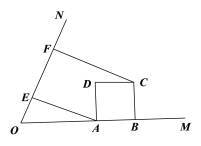
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
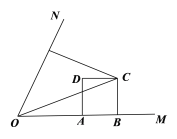
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
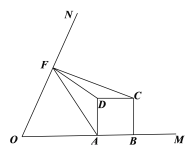
图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,已知∠BAC=90°,AB=6,AC=8,点D是AC上的一点,将△ABC沿着过点D的一条直线翻折,使点C落在BC边上的点E处,连接AE、DE,当∠CDE=∠AEB时,AE的长是______.
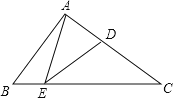
查看答案和解析>>
科目:初中数学 来源: 题型:
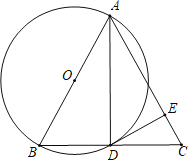
【题目】如图,△ABC中,AB=AC,AB是⊙O的直径,BC与⊙O交于点D,点E在AC上,且∠ADE=∠B.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此件文物进行复原,因此把残片抽象成了一个弓形,如图所示,经过测量得到弓形高CD=![]() 米,∠CAD=30°,请你帮助文物学家完成下面两项工作:
米,∠CAD=30°,请你帮助文物学家完成下面两项工作:
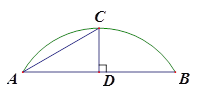
(1)作出此文物轮廓圆心O的位置(尺规作图,保留作图痕迹,不写作法);
(2)求出弓形所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com