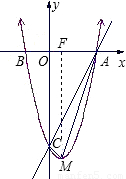
已知直线y=2x-4与x轴交于点A,与y轴交于点C,抛物线过点A,C和另一点B(-1,0).
(1)求此抛物线的解析式,并画出它的图象;
(2)在直线AC上求一点P,使以点A,B,P为顶点的三角形与△AOC相似;
(3)设抛物线的顶点为M,在抛物线上是否存在点Q,使△ABQ的面积等于△AMC的面积的4倍?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
分析:(1)根据已知直线的解析式,可求得A、C的坐标,然后根据A、B、C三点坐标,可利用待定系数法求出该抛物线的解析式.
(2)在Rt△AOC中,OC=2OA,若以点A,B,P为顶点的三角形与△AOC相似,那么△ABP也必为直角三角形,且直角边的比为1:2,由于∠BAP不是直角,因此要分类两种情况考虑:
①∠ABP=90°,过B作x轴的垂线,交直线AC于P,此时BP=2AB,符合题意,将B点横坐标代入直线AC的解析式中,即可得到点P的坐标;
②∠APB=90°,过B作直线AC的垂线,此时BP=2AP,也符合题意,过P作PH⊥x轴于H,首先根据相似三角形:Rt△AOC∽Rt△APB求出AP的长,进而根据Rt△APH∽Rt△ABP求出AH的长,从而根据OH=OA-AH求得P点横坐标,将其代入直线AC的解析式中,即可得到P点坐标.
(3)根据抛物线的解析式,易求得顶点M的坐标,分析图形,可过M作MF⊥x轴,由梯形MCOF、△AFM的面积和再减去△AOC的面积就可得到△AMC的面积,进而可求出△ABQ的面积,而AB的长易求得,根据三角形的面积公式,即可求得Q点纵坐标的绝对值,将其代入抛物线的解析式中,即可得到Q点坐标.
解答: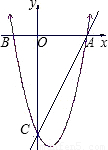
解:(1)令x=0,则y=-4;令y=0,则2x-4=0,从而x=2,
∴A点坐标为(2,0),C点坐标为(0,-4);
∵抛物线过点A(2,0),B(-1,0),
∴y=a(x-2)(x+1),(2分)
又抛物线过点C(0,-4),
∴a•(-2)×1=-4,
∴a=2;(3分)
∴所求抛物线的解析式为y=2(x-2)(x+1)=2x
2-2x-4.(4分)
∵
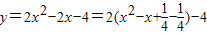
=
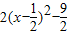
,
∴它的图象如图所示;(5分)
(2)∵△AOC是直角三角形,且|OA|=2,|OC|=4,
所作三角形必须是直角三角形,且两直角边的比是1:2;
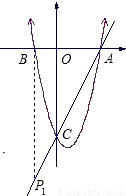
①如图,过点B作BP
1⊥x轴,交直线AC于P
1,(6分)
则由BP
1∥OC知Rt△ABP
1∽Rt△AOC;
∴P
1点的横坐标是-1,
∴P
1点的纵坐标是y=2×(-1)-4=-6;
∴P
1点的坐标是(-1,-6).(7分)
②∵|OA|=2,|OC|=4,
∴
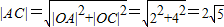
;
作BP
2⊥AC于P
2,如图,(8分)
∵∠AOC=90°,∠AP
2B=90°,又∠CAO=∠BAP
2,
∴Rt△AOC∽Rt△AP
2B;
∴
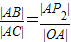
,
∴
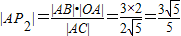
;
作P
2H⊥AB于H,则Rt△AP
2H∽Rt△ABP
2;
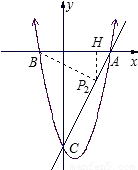
∴
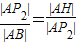
,
∴
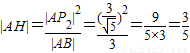
;
∴
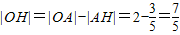
;(9分)
把
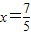
代入y=2x-4,得
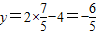
;
∴P
2点的坐标为
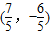
;
∴在直线AC上存在两点P
1(-1,-6),

,使△ABP与△AOC相似.(10分)
(3)∵抛物线的顶点是
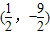
,
∴它的对称轴是直线
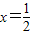
.(11分)
假设在抛物线y=2x
2-2x-4上存在点Q,使S
△ABQ=4S
△AMC;
设点Q的坐标为(x
,y
),对称轴与x轴交于
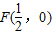
,
则S
△AMC=S
四边形AOCM-S
△AOC=S
△AFM+S
梯形FOCM-S
△AOC
=
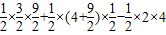
=
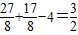
;(12分)
又△ABQ的面积S
△ABQ满足S
△ABQ=4S
△AMC∴
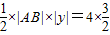
∴
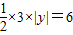
,
∴|y
|=4,
∴y
=±4;(13分)
当y
=4时,2x
2-2x-4=4,即x
2-x-4=0,
解之得
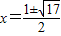
;
当y
=-4时,2x
2-2x-4=-4即2x
2-2x=0,
解之得x=0或x=1;
因此,在抛物线y=2x
2-2x-4上存在点Q,使S
△ABQ=4S
△AMC,此时点Q的坐标为
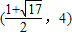
,
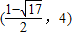
,
(0,-4),(1,-4).(14分)
(注:表示“线段的长”不用“||”号,均不扣分)
点评:此题主要考查了二次函数解析式的确定、相似三角形的判定和性质、图形面积的求法等知识,(2)题中,由于相似三角形的对应角和对应边不确定,一定要分类讨论,以免漏解.

 解:(1)令x=0,则y=-4;令y=0,则2x-4=0,从而x=2,
解:(1)令x=0,则y=-4;令y=0,则2x-4=0,从而x=2,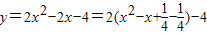 =
=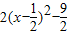 ,
,
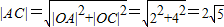 ;
;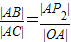 ,
,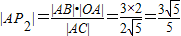 ;
;
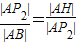 ,
,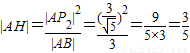 ;
;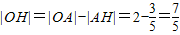 ;(9分)
;(9分)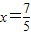 代入y=2x-4,得
代入y=2x-4,得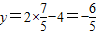 ;
;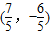 ;
; ,使△ABP与△AOC相似.(10分)
,使△ABP与△AOC相似.(10分)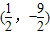 ,
,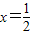 .(11分)
.(11分)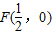 ,
,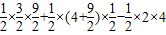 =
=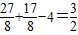 ;(12分)
;(12分)
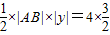
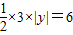 ,
,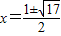 ;
;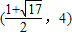 ,
,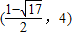 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案