
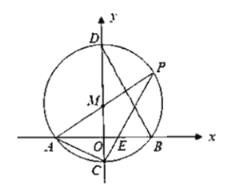
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨≈◊ŒÔœşy=ax2+8ax(a>0)”Îx÷·Ωª”ĞO£¨A¡Ωµ„£¨∂•µ„Œ™M£¨∂‘≥∆÷·”Îx÷·Ωª”ĞH£¨”Îπ˝O£¨A£¨M»˝µ„µƒ°—QΩª”е„B£¨°—Qµƒ∞Îæ∂Œ™5£¨µ„C¥”µ„B≥ˆ∑¢£¨—ÿ◊≈‘≤÷İÀ≥ ±’Μڵ„M‘À∂Ø£¨…‰œşMC”Îx÷·Ωª”ĞD£¨”Î≈◊ŒÔœşΩª”ĞE£¨π˝µ„E◊˜MEµƒ¥πœşΩª≈◊ŒÔœşµƒ∂‘≥∆÷·”е„F.
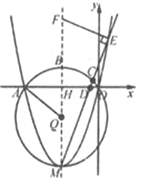
(1)«Û≈◊ŒÔœşµƒΩ‚Œˆ Ω£ª
(2)µ±µ„Cµƒ‘À∂ج∑æ∂≥§Œ™![]() ±£¨«Û÷§£∫HD=2
±£¨«Û÷§£∫HD=2![]() HA.
HA.
(3)‘е„C‘À∂Øπ˝≥Ã÷–£Æ «∑ҥʑВ‚—˘µƒŒª÷√£¨ πµ√“‘µ„M£¨E£¨FŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜AHQœ‡À∆?»Ù¥Ê‘Ğ£¨«Û≥ˆ¥ÀŒª÷√ ±µ„Eµƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”….
°æ¥∞∏°ø(1)y=![]() x2+4x£ª(2)÷§√˜º˚Ω‚Œˆ£ª(3)¥Ê‘Ğ£¨E(
x2+4x£ª(2)÷§√˜º˚Ω‚Œˆ£ª(3)¥Ê‘Ğ£¨E(![]() £¨
£¨![]() )ªÚE(
)ªÚE(![]() £¨
£¨![]() )
)
°æΩ‚Œˆ°ø
(1)¿˚”√∫Ø ˝Ω‚Œˆ Ω£¨”…y=0ø…«Û≥ˆ≈◊ŒÔœş”Îx÷·µƒ¡ΩΩªµ„◊¯±Í£¨¿˚”√¥πæ∂∂®¿Ì«Û≥ˆAHµƒ≥§£¨‘Ÿ‘ĞRt°˜AHQ÷–£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆHQµƒ≥§£¨”…∞Îæ∂Œ™5£¨ø…«Û≥ˆµ„Mµƒ◊¯±Í£¨»ª∫ÛΩ´µ„Mµƒ◊¯±Íµƒ∫Ø ˝Ω‚Œˆ Ω£¨Ω®¡¢πÿ”Ğaµƒ∑Ω≥ã¨Ω‚∑Ω≥ëÛ≥ˆaµƒ÷µ.
(2)¿˚”√ª°≥§π´ Ω«Û≥ˆnµƒ÷µ£¨∏˘æı‘≤÷İΩ«∂®¿Ì«Û≥ˆ°œBMCµƒ∂» ˝£¨‘ĞRt°˜HMD÷–£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆHDµƒ≥§£¨‘Ÿ∏˘æıMH=2AH£¨ø…÷§µ√Ω·¬ğ.
(3)∑÷«ÈøˆÃ÷¬ğ£∫¢Ÿµ±°œEMF=°œHQA ±,°˜MEF°◊°˜QHA£¨¿˚”√œ‡À∆»˝Ω«–Œµƒ∂‘”¶±ş≥…±»¿˝«Û≥ˆHDµƒ≥§£¨ø…µ√µΩµ„Dµƒ◊¯±Í£¨‘Ÿ¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œşMDµƒ∫Ø ˝Ω‚Œˆ Ω£¨»ª∫Û«Û≥ˆ¡Ω∫Ø ˝µƒΩªµ„◊¯±Í£ª¢Ğµ±°œEMF=°œQAH ±,°˜MEF°◊°˜AHQ£¨¿˚”√œ‡À∆»˝Ω«–Œµƒ∂‘”¶±ş≥…±»¿˝«Û≥ˆHDµƒ≥§£¨ø…µ√µΩµ„Dµƒ◊¯±Í£¨‘Ÿ¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œşMDµƒ∫Ø ˝Ω‚Œˆ Ω£¨»ª∫Û«Û≥ˆ¡Ω∫Ø ˝µƒΩªµ„◊¯±Í£¨º¥ø…µ√µΩ∑˚∫œÃ‚“‚µƒµ„Eµƒ◊¯±Í.
Ω‚£∫(1)¡Óy=0,µ√ax2+8ax=0,Ω‚µ√x1=-8,x2=0£¨
°‡A(-8£¨0)
”…¥πæ∂∂®¿Ì,µ√AH=![]() AO=4,
AO=4,
‘ĞRt°˜AHQ÷–, HQ=![]() £¨
£¨
°‡HM=HQ+QM=3+5=8£¨
°‡M(-4£¨-8)
∞—M(-4,-8)¥˙»Î≈◊ŒÔœşµ√![]() £¨
£¨
Ω‚µ√a=![]() £¨
£¨
°‡≈◊ŒÔœşµƒΩ‚Œˆ ΩŒ™y=![]() x2+4x
x2+4x
(2)°şµ„Cµƒ¬∑æ∂Œ™![]() ,
,
°‡![]() £¨Ω‚µ√n=120°„£¨
£¨Ω‚µ√n=120°„£¨
°‡°œBMC=![]() =60°„,
=60°„,
‘ĞRt°˜HMD÷–, HD=![]() =
=![]() MH
MH
°şMH=8,AH=4,º¥MH=2HA
°‡HD=2![]() HA
HA
(3)¥Ê‘Ğ£¨Eµ„◊¯±ÍŒ™(![]() £¨
£¨![]() )ªÚ(
)ªÚ(![]() £¨
£¨![]() )£¨¿Ì”…»Áœ¬£∫
)£¨¿Ì”…»Áœ¬£∫
“—÷™°œFEM=°œAHQ=90°„£¨
¢Ÿµ±°œEMF=°œHQA ±,°˜MEF°◊°˜QHA,
¥À ±°˜MHD°◊°˜QHA,
°‡![]() ,º¥
,º¥![]()
Ω‚µ√HD=![]() £¨
£¨
°‡OD=![]()
°‡D(![]() 0)£¨
0)£¨
…Ë÷±œşMDΩ‚Œˆ ΩŒ™![]() £¨Ω´M(-4£¨-8)£¨D(
£¨Ω´M(-4£¨-8)£¨D(![]() 0)¥˙»Îµ√£¨
0)¥˙»Îµ√£¨
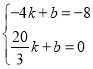 £¨Ω‚µ√
£¨Ω‚µ√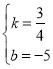 £¨
£¨
°‡÷±œşMDµƒΩ‚Œˆ ΩŒ™y=![]() x-5,
x-5,
Ω´÷±œşMD”Î≈◊ŒÔœş¡™¡¢µ√£¨
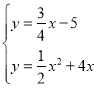 £¨Ω‚µ√
£¨Ω‚µ√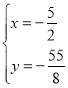 ªÚ
ªÚ![]()
¥À ±Eµ„◊¯±ÍŒ™(![]() £¨
£¨![]() )£ª
)£ª
¢Ğµ±°œEMF=°œQAH ±£¨°˜MEF°◊°˜AHQ,
¥À ±°˜MHD°◊°˜AHQ,
°‡![]() £¨º¥
£¨º¥![]()
Ω‚µ√HD=6£¨
°‡OD=6-4=2
°‡D(2,0),
…Ë÷±œşMDΩ‚Œˆ ΩŒ™![]() £¨Ω´M(-4£¨-8)£¨D(2£¨0)¥˙»Îµ√£¨
£¨Ω´M(-4£¨-8)£¨D(2£¨0)¥˙»Îµ√£¨
![]() £¨Ω‚µ√
£¨Ω‚µ√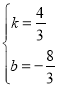 £¨
£¨
°‡÷±œşMDµƒΩ‚Œˆ ΩŒ™![]()
Ω´÷±œşMD”Î≈◊ŒÔœş¡™¡¢µ√£¨
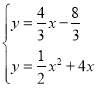 £¨Ω‚µ√
£¨Ω‚µ√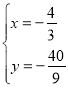 ªÚ
ªÚ![]()
¥À ±Eµ„◊¯±ÍŒ™(![]() £¨
£¨![]() )£ª
)£ª
◊ğ…œÀ˘ ˆ£¨Eµ„◊¯±ÍŒ™(![]() £¨
£¨![]() )ªÚ(
)ªÚ(![]() £¨
£¨![]() ).
).


 ∆Ѓ©∏¥œ∞ºÏ≤‚œµ¡–¥∞∏
∆Ѓ©∏¥œ∞ºÏ≤‚œµ¡–¥∞∏ ≥¨ƒİ—ßµ‰µ•‘™∆Ğ÷–∆Ѓ©◊®Ã‚≥Â¥Ã100∑÷œµ¡–¥∞∏
≥¨ƒİ—ßµ‰µ•‘™∆Ğ÷–∆Ѓ©◊®Ã‚≥Â¥Ã100∑÷œµ¡–¥∞∏ ª∆∏‘360∂»∂®÷∆√İæÌœµ¡–¥∞∏
ª∆∏‘360∂»∂®÷∆√İæÌœµ¡–¥∞∏ —Ùπ‚øº≥°µ•‘™≤‚ ‘æÌœµ¡–¥∞∏
—Ùπ‚øº≥°µ•‘™≤‚ ‘æÌœµ¡–¥∞∏ √˚–£¡™√À≥Â¥ÃæÌœµ¡–¥∞∏
√˚–£¡™√À≥Â¥ÃæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“‘µ„![]() Œ™‘≤–ƒ£¨◊˜
Œ™‘≤–ƒ£¨◊˜![]() Ωª
Ωª![]() ÷·”Ğ
÷·”Ğ![]() °¢
°¢![]() ¡Ωµ„£¨Ωª
¡Ωµ„£¨Ωª![]() ÷·”Ğ
÷·”Ğ![]() °¢
°¢![]() ¡Ωµ„£¨¡¨Ω·
¡Ωµ„£¨¡¨Ω·![]() ≤¢—”≥§Ωª
≤¢—”≥§Ωª![]() ”е„
”е„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() Ωª
Ωª![]() ÷·”е„
÷·”е„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨
£¨![]() .
.
£®1£©«Ûœ“![]() µƒ≥§£ª
µƒ≥§£ª
£®2£©«Û÷±œş![]() µƒ∫Ø ˝Ω‚Œˆ Ω£ª
µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®3£©¡¨Ω·![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝.
µƒ√ʪ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
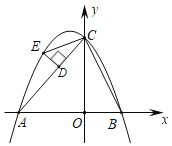
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœş”Î◊¯±Í÷·Ωª”ĞA£®©Å4£¨0£©°¢B£®2£¨0£©°¢C£®0£¨4£©£¨¡¨Ω”BC£¨AC£Æ
£®1£©«Û≈◊ŒÔœşµƒΩ‚Œˆ Ω£ª
£®2£©»Ùµ„E «≈◊ŒÔœş‘еĞ∂˛œÛœŞ…œµƒ“ªµ„£¨π˝µ„E◊˜DE°ÕAC”е„D£¨«ÛDEµƒ◊Ó¥Û÷µ£Æ
£®3£©»Ùµ„E «≈◊ŒÔœş…œµĞ∂˛œÛœŞ…œµƒ“ª∂ص„£¨π˝µ„E◊˜DE°ÕAC”е„D£¨¡¨Ω”CE£¨»Ù°˜CDE”ΰ˜COBœ‡À∆£¨÷±Ω”–¥≥ˆµ„Eµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæ‘к◊““¡ΩµÿÕ¨ ±œ˙ ğƒ≥÷÷∆∑≈∆µƒ∆˚≥µ£¨“—÷™‘к◊µÿµƒ◊İœ˙ ğ¿˚»Ûy£®µ•Œª£∫ÕÚ‘™£©”Îœ˙ ğ¡øx£®µ•Œª£∫¡æ£©÷ƺ‰¬˙◊„y£Ω©Å![]() x2+10x£¨‘Ğ““µÿ√øœ˙ 𓪡æ∆˚≥µø…ªÒµ√2ÕÚ‘™µƒœ˙ ğ¿˚»Û£¨»Ù∏√π´Àæ‘к◊““¡Ωµÿπ≤œ˙ ğ30¡æ∏√∆∑≈∆µƒ∆˚≥µ£¨º◊““¡Ωµÿ◊ݵƒœ˙ ğ¿˚»ÛŒ™WÕÚ‘™£¨∆‰÷–‘к◊µÿœ˙ ğx¡æ£Æ
x2+10x£¨‘Ğ““µÿ√øœ˙ 𓪡æ∆˚≥µø…ªÒµ√2ÕÚ‘™µƒœ˙ ğ¿˚»Û£¨»Ù∏√π´Àæ‘к◊““¡Ωµÿπ≤œ˙ ğ30¡æ∏√∆∑≈∆µƒ∆˚≥µ£¨º◊““¡Ωµÿ◊ݵƒœ˙ ğ¿˚»ÛŒ™WÕÚ‘™£¨∆‰÷–‘к◊µÿœ˙ ğx¡æ£Æ
£®1£©«ÛW”Îxµƒ∫Ø ˝πÿœµ Ω£ª
£®2£©º◊““¡Ωµÿ∏˜œ˙ ğ∂‡…Ÿ¡æ≥µ ±W◊Ó¥Û£øWµƒ◊Ó¥Û÷µ «∂‡…Ÿ£ø
£®3£©Œ™¡Àø™Õÿº◊µÿ –≥°£¨π´ÀæπÊ∂®º◊µÿ∆Ωæ˘√ø¡æ∆˚≥µµƒœ˙ ğ¿˚»Û≤ª∏ş”Ğ2ÕÚ‘™£¨ƒ«√¥π´Àæœ˙ ğ’‚30¡æ∆˚≥µø…ªÒµ√µƒ◊Ó¥Ûœ˙ ğ¿˚»Û «∂‡…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœşy=x2-(m+1)x+m”Îy÷·Ωª”Ğ(0£¨-3)µ„.
(1)«Û≥ˆmµƒ÷µ∫Õ≈◊ŒÔœş”Îx÷·µƒΩªµ„£ª
(2)x»° ≤√¥÷µ ±£¨y>0.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨PA°¢PBŒ™‘≤Oµƒ«–œş£¨«–µ„∑÷±Œ™A°¢B£¨POΩªAB”е„C£¨POµƒ—”≥§œşΩª‘≤O”е„D£¨œ¬¡–Ω·¬ğ≤ª“ª∂®≥…¡¢µƒ «( )
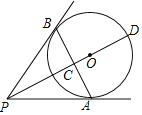
A. PA£ΩPBB. °œBPD£Ω°œAPDC. AB°ÕPDD. AB∆Ω∑÷PD
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬±Ìœ‘ 浃 «ƒ≥÷÷¥Û∂π‘Ğœ‡Õ¨Ãº˛œ¬µƒ∑¢—ø ‘—ÈΩ·π˚£∫
√ø≈˙¡£ ˝n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
∑¢—øµƒ¡£ ˝m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
∑¢—øµƒ∆µ¬ | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
œ¬√Ê”–»˝∏ˆÕ∆∂œ£∫
¢Ÿµ±nŒ™400 ±£¨∑¢—øµƒ¥Û∂π¡£ ˝Œ™382£¨∑¢—øµƒ∆µ¬ Œ™0.955£¨À˘“‘¥Û∂π∑¢—øµƒ∏≈¬ «0.955£ª
¢ĞÀÊ◊≈ ‘—È ±¥Û∂πµƒ¡£ ˝µƒ‘ˆº”£¨¥Û∂π∑¢—øµƒ∆µ¬ ◊İ‘Ğ0.95∏ΩΩ¸∞Ğ∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆¥Û∂π∑¢—øµƒ∏≈¬ «0.95£ª
¢ğ»Ù¥Û∂π¡£ ˝nŒ™4000£¨π¿º∆¥Û∂π∑¢—øµƒ¡£ ˝¥Û‘ºŒ™3800¡££Æ
∆‰÷–Õ∆∂œ∫œ¿Ìµƒ «£®°°°°£©
A. ¢Ÿ¢Ğ¢ğ B. ¢Ÿ¢Ğ C. ¢Ÿ¢ğ D. ¢Ğ¢ğ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
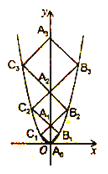
°æƒø°ø∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ»ÁÕº£¨µ„
µƒÕºœÛ»ÁÕº£¨µ„![]() Œª”Ğ◊¯±Í‘≠µ„£¨µ„
Œª”Ğ◊¯±Í‘≠µ„£¨µ„![]() ‘Ğ
‘Ğ![]() ÷·µƒ’˝∞Î÷·…œ£¨µ„
÷·µƒ’˝∞Î÷·…œ£¨µ„![]() ‘Ğ∂˛¥Œ∫Ø ˝Œª”еГªœÛœŞµƒÕºœÛ…œ£¨µ„
‘Ğ∂˛¥Œ∫Ø ˝Œª”еГªœÛœŞµƒÕºœÛ…œ£¨µ„![]() ‘Ğ∂˛¥Œ∫Ø ˝Œª”еĞ∂˛œÛœŞµƒÕºœÛ…œ£¨Àƒ±ş–Œ
‘Ğ∂˛¥Œ∫Ø ˝Œª”еĞ∂˛œÛœŞµƒÕºœÛ…œ£¨Àƒ±ş–Œ![]() £¨Àƒ±ş–Œ
£¨Àƒ±ş–Œ![]() £¨Àƒ±ş–Œ
£¨Àƒ±ş–Œ![]() °≠Àƒ±ş–Œ
°≠Àƒ±ş–Œ![]() ∂º «’˝∑Ω–Œ£¨‘Ú’˝∑Ω–Œ
∂º «’˝∑Ω–Œ£¨‘Ú’˝∑Ω–Œ![]() µƒ÷İ≥§Œ™__________.
µƒ÷İ≥§Œ™__________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨AB «![]() µƒ÷±æ∂£¨C «∞Α≤AB…œ“ªµ„£¨¡¨AC°¢OC£¨AD∆Ω∑÷
µƒ÷±æ∂£¨C «∞Α≤AB…œ“ªµ„£¨¡¨AC°¢OC£¨AD∆Ω∑÷![]() £¨Ωªª°BC”ĞD£¨ΩªOC”ĞE£¨¡¨OD£¨CD£¨œ¬¡–Ω·¬ğ£∫
£¨Ωªª°BC”ĞD£¨ΩªOC”ĞE£¨¡¨OD£¨CD£¨œ¬¡–Ω·¬ğ£∫
¢Ÿª°![]() ª°CD£ª¢Ğ
ª°CD£ª¢Ğ![]() £ª¢ğ
£ª¢ğ![]() £ª¢İµ±C «∞Α≤
£ª¢İµ±C «∞Α≤![]() µƒ÷–µ„ ±£¨‘Ú
µƒ÷–µ„ ±£¨‘Ú![]() £Æ∆‰÷–’˝»∑µƒΩ·¬ğ «£® £©
£Æ∆‰÷–’˝»∑µƒΩ·¬ğ «£® £©
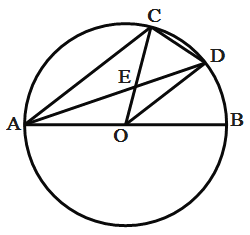
A.¢Ÿ¢Ğ¢ğB.¢Ÿ¢Ğ¢İC.¢Ÿ¢ğ¢İD.¢Ğ¢ğ¢İ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com