
【题目】[阅读理解]
我们知道:![]() ,那么
,那么![]() 结果等于多少呢?
结果等于多少呢?
在图1所示的等边三角形数阵中,第![]() 行的一个小等边三角形中的数为
行的一个小等边三角形中的数为![]() ,即
,即![]() 第
第![]() 行的三个小等边三角形中的数的和是
行的三个小等边三角形中的数的和是![]() 即
即![]() ; ..第
; ..第![]() 行的
行的![]() 个小等边三角形中的数的和是
个小等边三角形中的数的和是![]() 个,即
个,即![]() ,该等边三角形数阵中共有
,该等边三角形数阵中共有![]() 小等边三角形,所有小等边三角形数的和为
小等边三角形,所有小等边三角形数的和为![]() .
.
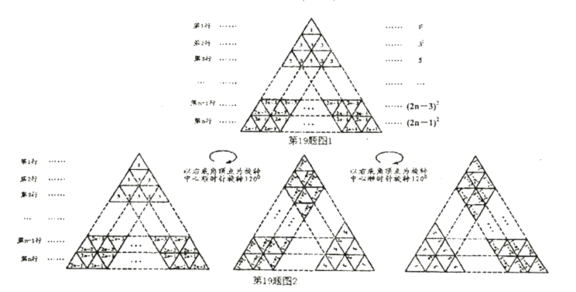
[规律探究]
以图1中的等边三角形数阵的右底角顶点为旋转中心顺时针旋转![]() 再把旋转后的图形按同样的方法可得如图2所示的三角形数阵,观察这三个等边三角形数阵各行同一位置的小等边三角形中的数,发现位于奇数位置的三个数(如第
再把旋转后的图形按同样的方法可得如图2所示的三角形数阵,观察这三个等边三角形数阵各行同一位置的小等边三角形中的数,发现位于奇数位置的三个数(如第![]() 行的第
行的第![]() 个小三角形中的数分别为
个小三角形中的数分别为![]() 的和为
的和为![]() ;发现位于偶数位置的三个数(如第
;发现位于偶数位置的三个数(如第![]() 行的第
行的第![]() 个小三角形中的数分别为
个小三角形中的数分别为![]() 的和为
的和为![]() ;而每个等边三角形数阵中,由于位于奇数位置的数比位于偶数位置的数多
;而每个等边三角形数阵中,由于位于奇数位置的数比位于偶数位置的数多![]() 个,则位于偶数位置的数有_
个,则位于偶数位置的数有_
个![]()
因此,![]()
[解决问题]根据以上发现,计算:![]()
【答案】[规律探究]![]() ,
,![]() ,
,![]() ,
,![]() ;[解决问题]
;[解决问题]![]()
【解析】
[规律探究] 设每个等边三角形数阵中位于偶数位置的数有x个,根据题意列出方程即可求出x的值,从而求出每个等边三角形数阵中位于奇数位置的数的个数,再根据题意,即可求出这三个等边三角形数阵所有数的总和,即可求出最终结论;
[解决问题] 令2n-1=2019,即可求出n的值,然后代入[规律探究]的公式即可求出结论.
解:[规律探究]设每个等边三角形数阵中位于偶数位置的数有x个,
由题意可得x+(x+n)=n2
解得:x=![]() ,
,
则每个等边三角形数阵中位于奇数位置的数有![]() +n=
+n=![]()
∴由此可得,这三个等边三角形数阵所有数的总和为: ![]() (4n+1)×
(4n+1)×![]() +(4n-1)×
+(4n-1)×![]() =
=![]()
∴![]()
![]()
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
[解决问题] 令2n-1=2019
解得:n=1010
![]()
=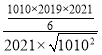
=![]()
![]()


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,菱形![]() 的顶点
的顶点![]() 、
、![]() 在菱形
在菱形![]() 的边上,且
的边上,且![]() ,请直接写出
,请直接写出![]() 的结果(不必写计算过程)
的结果(不必写计算过程)
(2)将图1中的菱形![]() 绕点
绕点![]() 旋转一定角度,如图2,求
旋转一定角度,如图2,求![]() ;
;
(3)把图2中的菱形都换成矩形,如图3,且![]() ,此时
,此时![]() 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
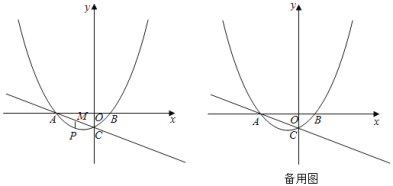
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定一个函数,如果这个函数的图象上存在一个点,它的横、纵坐标相等,那么这个点叫做该函数的不变点.
(1)一次函数![]() 的不变点的坐标为______.
的不变点的坐标为______.
(2)二次函数![]() 的两个不变点分别为点
的两个不变点分别为点![]() (
(![]() 在
在![]() 的左侧),将点
的左侧),将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)已知二次函数![]() 的两个不变点的坐标为
的两个不变点的坐标为![]() .
.
①求![]() 的值;
的值;
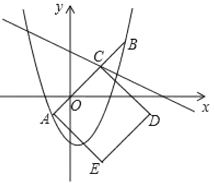
②如图,设抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .点
.点![]() 为一次函数
为一次函数![]() 的不变点,以线段
的不变点,以线段![]() 为边向下作正方形
为边向下作正方形![]() .当
.当![]() 两点中只有一个点在封闭图形
两点中只有一个点在封闭图形![]() 的内部(不包含边界)时,求出
的内部(不包含边界)时,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
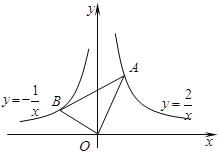
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.7);
≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
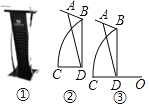
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内,![]() .
.
(1)如图1,若![]() ,
,![]() ,
,![]() ,点,
,点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 递时针旋转一定角度,得到
递时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长变
并延长变![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,若![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 、
、![]() 、
、![]() 之间的关系(不需要证明).
之间的关系(不需要证明).
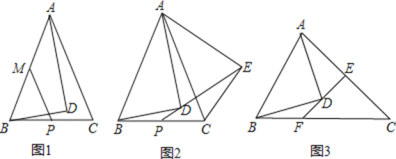
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵![]() 元,用
元,用![]() 元购进乙书包的个数与用
元购进乙书包的个数与用![]() 元购进甲书包的个数相等.
元购进甲书包的个数相等.
(1)求甲、乙两种书包的进价分别为多少元?
(2)商户购进甲、乙两种书包共![]() 个进行试销,其中甲书包的个数不少于
个进行试销,其中甲书包的个数不少于![]() 个,且甲书包的个数 的
个,且甲书包的个数 的![]() 倍不大于乙书包的个数,已知甲书包的售价为
倍不大于乙书包的个数,已知甲书包的售价为![]() 元/个,乙书包的售价为
元/个,乙书包的售价为![]() 元/个,且 全部售出,设购进甲书包
元/个,且 全部售出,设购进甲书包![]() 个,求该商店销售这批书包的利润
个,求该商店销售这批书包的利润![]() 与
与![]() 之间的函数关系式,并 写出
之间的函数关系式,并 写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,该店将![]() 个书包全部售出后,使用所获的利润又购进
个书包全部售出后,使用所获的利润又购进![]() 个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利
个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利![]() 元.请求出该店第二次进货所选用的进货方案?
元.请求出该店第二次进货所选用的进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com