
已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
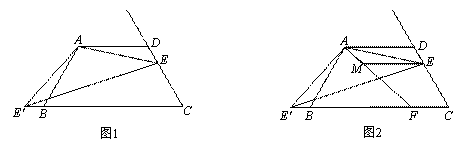
(1)如图1,∠AEE'= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=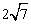 ,求ME的长.
,求ME的长.

解:(1) 30°.
(2)当点E在线段CD上时,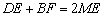 ;
;
当点E在CD的延长线上,
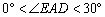 时,
时,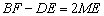 ;
;
 时,
时,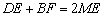 ;
;
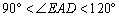 时,
时,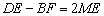 .
.
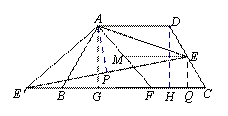
(3)作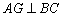 于点G, 作
于点G, 作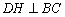 于点H.
于点H.
由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°,
易知四边形AGHD是矩形和两个全等的直角三角形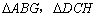 .
.
则GH=AD , BG=CH.
∵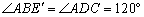 ,
,
∴点 、B、C在一条直线上.
、B、C在一条直线上.
设AD=AB=CD=x,则GH=x,BG=CH=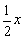 ,.
,.
 作
作 于Q.
于Q.
在Rt△EQC中,CE=2,  ,
,
∴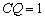 ,
, 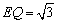 .
.
∴E'Q=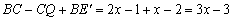 .
.
作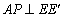 于点P.
于点P.
∵△ADE绕点A顺时针旋转120°后,得到△ABE'.
∴△A EE'是等腰三角形,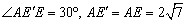 .
.
∴在Rt△AP E'中,E'P= .
.
∴EE'=2 E'P=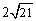 .
.
∴在Rt△EQ E'中,E'Q=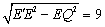 .
.
∴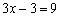 .
.
∴ .
.
∴ ,
,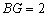 .
.
∴
在Rt△E'AF中,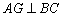 ,
,
∴Rt△AG E'∽Rt△FA E'.
∴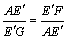
∴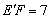 .
.
∴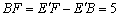 .
.
由(2)知: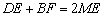 .[来源:Z*xx*k.Com]
.[来源:Z*xx*k.Com]
∴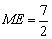 .
.


科目:初中数学 来源: 题型:
将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
|
| A. y=(x﹣2)2 | B. | y=(x﹣2)2+6 | C. | y=x2+6 | D. | y=x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确 到
到 ,
, ).
).


查看答案和解析>>
科目:初中数学 来源: 题型:
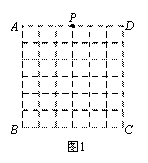
如图1,正方形ABC D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.
D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.
(1)请在图中画出点P经过的路径;
(2)求点P经过的路径总长.
 | |||
 | |||
| |
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)已知二次函数 ,请你化成
,请你化成 的形式,并在直角坐标系中画出
的形式,并在直角坐标系中画出 的图象;
的图象;
(2)如果 ,
, 是(1)中图象上的两点,且
是(1)中图象上的两点,且 ,请直接写出
,请直接写出 、
、 的大小关系;
的大小关系;
(3)利用(1)中的图象表示出方程 的根来,要求保留画图痕迹,说明结果.
的根来,要求保留画图痕迹,说明结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件 中,为必然事件的是
中,为必然事件的是
A.购买一张彩票,一定中奖. B.一个袋中只装有5个黑球,从中摸出一个球是黑球.
C.抛掷一枚硬币,正面向上. D.打开电视,正在播放广告.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,圆心B在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1).过点P(0,-7)的直线l与⊙B相交于C、D两点,则弦CD长的所有可能的整数值有_______个;它们是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明口袋中装有除颜色不同外其它都完全相同的小球,其中白球2个,红球3个,黄球5个,将它们搅匀后从袋中随机摸出1个球,则摸出黄球的概率是 ( )
A.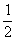 B.
B. C.
C.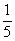 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
一次函数y=(k-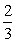 )x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求k的值;
(2)若一抛物线经过点A、B、C三点,求此抛物线的解析式。
(3)当抛物线开口向上时过A、B、C三点作△ABC,求tan∠ABC的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com