
【题目】已知,抛物线![]() 与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
(1)求k值;
(2)该抛物线与直线![]() 交于C、D两点,求S△ACD;
交于C、D两点,求S△ACD;
(3)该抛物线上是否存在不同于A点的点P,使S△PCD=S△ACD?若存在,求出P点坐标.
(4)若该抛物线上有点P,使S△PCD=tS△ACD,抛物线上满足条件的P点有2个,3个,4个时,分别直接写出t的取值范围.
【答案】(1)k=4(2)![]() (3)存在符合条件的P点,且坐标为 P1(7,
(3)存在符合条件的P点,且坐标为 P1(7,![]() )、P2(
)、P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );(4)当0<t<
);(4)当0<t<![]() 时,P点有四个;当t=
时,P点有四个;当t=![]() 时,P点有三个;当t>
时,P点有三个;当t>![]() 时,P点有两个
时,P点有两个
【解析】
(1)设A(x1,0)、B(x2,0),x1、x2>0,根据题意可得AB=|x1﹣x2|=![]() =4,而x1+x2,x1x2可由k表达出来,根据等量关系即可求得k的值;
=4,而x1+x2,x1x2可由k表达出来,根据等量关系即可求得k的值;
(2)先联立直线CD和抛物线的解析式求出C,D两点的坐标,此时从图可看出△ACD是一个不规则的三角形,所以可过A作直线AE∥y轴,交直线CD于E,那么线段AE为底,C,D的横坐标差的绝对值为高即可得出△ACD的面积;
(3)设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L,那么直线l1,l2到直线CD的距离等于点A到直线CD的距离,所以它们与抛物线的交点都是符合条件的P点;
(4)通过作图可以发现,在直线CD上方肯定有两个P点,所以只考虑直线CD下方的P点数,这就要抓住P点有三个或CD下方有一个P点的情况:P为平行于CD的直线与抛物线的唯一交点;若上述情况(P点有三个)中,t=![]() ,那么:P点有两个时,t>
,那么:P点有两个时,t>![]() ;P点有四个时,0<t<
;P点有四个时,0<t<![]() .
.
(1)设A(x1,0)、B(x2,0),且x1<x2,x1、x2>0,
则:x1+x2=2k,x1x2=2(k+2)=2k+4,
∴AB=|x1﹣x2|=![]() =4,即:k2﹣2k﹣8=0,
=4,即:k2﹣2k﹣8=0,
解得:k1=﹣2,k2=4,
∵x1+x2>0,即k>0,
∴k=4;
(2)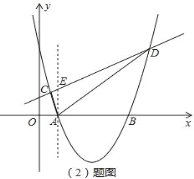
由(1)知,抛物线的解析式:y=![]() x2﹣4x+6,点A(2,0),B(6,0);
x2﹣4x+6,点A(2,0),B(6,0);
联立直线CD和抛物线的解析式,有:
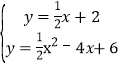 ,
,
解得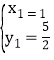 ,
,![]() ,
,
即:C(1,![]() ),D(8,6),
),D(8,6),
如图,过A作直线AE∥y轴,交直线CD于E,则E(2,3),AE=3,
S△ACD=![]() AE×|xD﹣xC|=
AE×|xD﹣xC|=![]() ×3×7=
×3×7=![]() ;
;
(3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;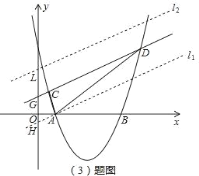
设直线l1:y=![]() x+b1,代入A(2,0),得:
x+b1,代入A(2,0),得:
![]() ×2+b1=0,b1=﹣1
×2+b1=0,b1=﹣1
即,直线l1:y=![]() x﹣1,H(0,﹣1),GL=GH=3,L(0,5);
x﹣1,H(0,﹣1),GL=GH=3,L(0,5);
同上,可求得,直线l2:y=![]() x+5;
x+5;
联立直线l1与抛物线的解析式,得:
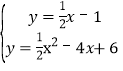 ,
,
解得![]() ,
,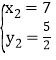 ,
,
即:P1(7,![]() );
);
联立直线l2与抛物线的解析式,得:
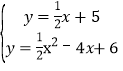 ,
,
解得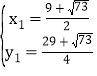 ,
,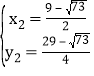 ,
,
即:P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );
);
综上,存在符合条件的P点,且坐标为 P1(7,![]() )、P2(
)、P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );
);
(4)当满足条件的P点有三个时,如右图: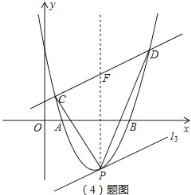
直线l3∥CD,且直线l3与抛物线只有唯一交点P;
设直线l3:y=![]() x+b3,联立抛物线的解析式有:
x+b3,联立抛物线的解析式有:
![]() x+b3=
x+b3=![]() x2﹣4x+6,即:x2﹣9x+12﹣2b3=0
x2﹣4x+6,即:x2﹣9x+12﹣2b3=0
△=81﹣4×(12﹣2b3)=0,解得:b3=﹣![]()
即,直线l3:y=![]() x﹣
x﹣![]() ,P(
,P(![]() ,﹣
,﹣![]() );
);
过点P作直线PF∥y轴,交直线CD于F,则F(![]() ,
,![]() )、PF=
)、PF=![]() ,
,
S△PCD=![]() PF×|yD﹣yC|=
PF×|yD﹣yC|=![]() ×
×![]() ×7=
×7=![]() ,t=
,t=![]() =
=![]() =
=![]() ,
,
综上上面的计算结果和图形来看:
当0<t<![]() 时,P点有四个;
时,P点有四个;
当t=![]() 时,P点有三个;
时,P点有三个;
当t>![]() 时,P点有两个.
时,P点有两个.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011内蒙古赤峰,7,3分)早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )

A.小张去时所用的时间多于回家所用的时间B.小张在公园锻炼了20分钟
C.小张去时的速度大于回家的速度 D.小张去时走上坡路,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )

A. 196 B. 195 C. 132 D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D 为∠BAC 的外角平分线上一点并且满足 BD=CD, 过 D 作 DE⊥AC 于 E,DF⊥AB 交 BA 的延长线于 F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有______

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com