
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
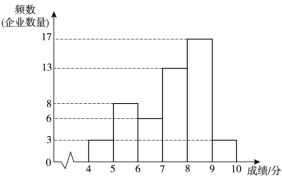
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
【答案】(1)7.84;(2)B,见解析(3)290
【解析】
(1)根据中位数定义,先把50名企业A项指标成绩排序,而中位数就是第25,26两项数据的平均数,易得(7.82+7.86)÷ 2 =7.84,即求出m的值;
(2)结合![]() 两项指标成绩的平均数、中位数、众数综合评判:该企业A项指标成绩是7.5分,小于A项指标成绩的中位数,说明该企业A项指标成绩的排名在后25名;B项指标成绩是7.5分,大于B项指标成绩的中位数,说明该企业B项指标成绩的排名在前25名,故让该企业成绩排名更靠前的指标是B.
两项指标成绩的平均数、中位数、众数综合评判:该企业A项指标成绩是7.5分,小于A项指标成绩的中位数,说明该企业A项指标成绩的排名在后25名;B项指标成绩是7.5分,大于B项指标成绩的中位数,说明该企业B项指标成绩的排名在前25名,故让该企业成绩排名更靠前的指标是B.
(3)先根据样本数据计算出样本中A项指标成绩超过7.68分的企业数量,再表示这部分在样本中的占比为![]() ,再用该地区的企业总数乘以
,再用该地区的企业总数乘以![]() ,即可估算出该地区A项指标成绩超过7.68分的企业数量.
,即可估算出该地区A项指标成绩超过7.68分的企业数量.
解:(1)根据中位数的定义,把50名企业A项指标成绩排序,
可得第25,26两项数据分别是7.82 和 7.86,
∴中位数为(7.82+7.86)÷ 2 =7.84
故m = 7.84.
(2)在此次调研评估中,该企业成绩排名更靠前的指标是B.
理由:该企业A项指标成绩是7.5分,小于A项指标成绩的中位数,说明该企业A项指标成绩的排名在后25名;B项指标成绩是7.5分,大于B项指标成绩的中位数,说明该企业B项指标成绩的排名在前25名.
(3)根据题意可知,在样本中,由(1)排序知,A项指标成绩在![]() 这一组,A项指标成绩超过7.68分的企业数量是9,A项指标成绩在
这一组,A项指标成绩超过7.68分的企业数量是9,A项指标成绩在![]() 这一组的数量是17,A项指标成绩在
这一组的数量是17,A项指标成绩在![]() 这一组的数量是3
这一组的数量是3
∴9+17+3=29,
∴估计该地区A项指标成绩超过7.68分的企业数量为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE 、DF.

(1)判断四边形BEDF的形状,并说明理由;
(2)若AB=8,AD=16,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,
上,![]() .点
.点![]() 为边
为边![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
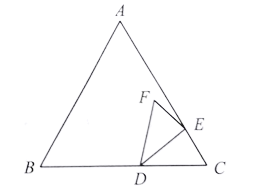
(1)当点![]() 在
在![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(3)连接![]() 设
设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 记
记![]()
![]() 是否存在最大值?若存在,请直接写出
是否存在最大值?若存在,请直接写出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 与点
与点![]() 分别位于直线
分别位于直线![]() 的两侧,且
的两侧,且![]() ,连接
,连接![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,
①当![]() 时,设
时,设![]() (其中
(其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积),求
的面积),求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
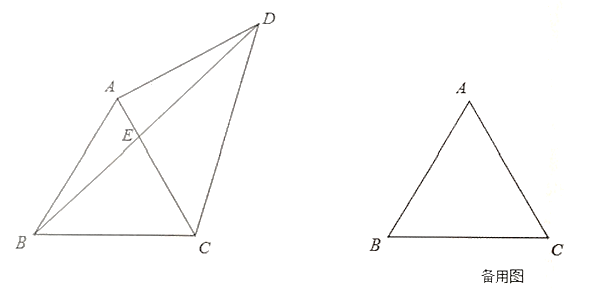
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
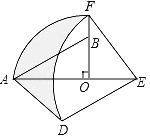
查看答案和解析>>
科目:初中数学 来源: 题型:
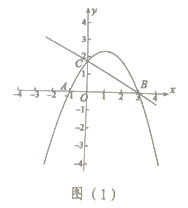
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
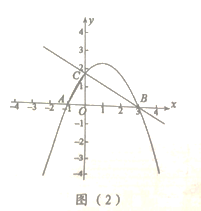
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
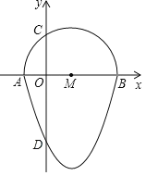
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点![]() 、
、![]() 、
、![]() 、
、![]() 分别是“果圆”与坐标轴的交点,抛物线的解析式为
分别是“果圆”与坐标轴的交点,抛物线的解析式为![]() ,
,![]() 为半圆的直径,则这个“果圆”被
为半圆的直径,则这个“果圆”被![]() 轴截得的弦
轴截得的弦![]() 的长为_________.
的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com