
如图,抛物线 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
(1)求该抛物线的解析式;
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
解:(1)把点C(0,-4),B(2,0)分别代入 中,
中,
得 ,解得
,解得 。
。
∴该抛物线的解析式为 。
。
(2)令y=0,即 ,解得x1=-4,x2=2。
,解得x1=-4,x2=2。
∴A(﹣4,0),S△ABC= AB•OC=12。
AB•OC=12。
设P点坐标为(x,0),则PB=2﹣x。
∵PE∥AC,∴∠BPE=∠BAC,∠BEP=∠BCA。∴△PBE∽△ABC。
∴ ,即
,即 ,化简得:
,化简得: 。
。
∴
 。
。
∴当x=﹣1时,S△PCE的最大值为3。
(3)△OMD为等腰三角形,可能有三种情形:
①当DM=DO时,如图①所示,
∵DO=DM=DA=2,
∴∠OAC=∠AMD=45°。∴∠ADM=90°。
∴M点的坐标为(-2,-2)。
②当MD=MO时,如图②所示,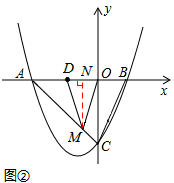
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3。
∴M点的坐标为(-1,-3)。
③当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为 ×4=
×4= ,即AC上的点与点O之间的最小距离为
,即AC上的点与点O之间的最小距离为 。
。
∵ >2,∴OD=OM的情况不存在。
>2,∴OD=OM的情况不存在。
综上所述,点M的坐标为(-2,-2)或(-1,-3)。
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
如图,一次函数y=kx+n的图象与x轴和y轴分别交于点A(6,0)和B(0, ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.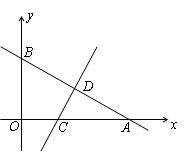
(1)试确定这个一次函数解析式;(3分)
(2)求过A、B、C三点的抛物线的函数关系式;(6分)
(3)请你利用所求抛物线的图像回答:当x取何值时,抛物线中的部分图像落在x轴的上方? (3分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系中,点A的坐标为( ,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.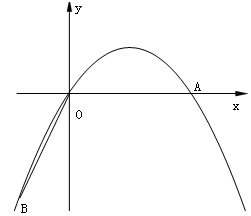
(1)请直接写出点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)如果点P是(2)中的抛物线上的动点,且在x轴的上方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,已知抛物线C经过原点,对称轴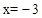 与抛物线相交于第三象限的点M,与x轴相交于点N,且
与抛物线相交于第三象限的点M,与x轴相交于点N,且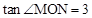 。
。
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转1800得到抛物线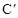 ,抛物线
,抛物线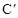 与x轴的另一交点为A,B为抛物线
与x轴的另一交点为A,B为抛物线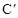 上横坐标为2的点。
上横坐标为2的点。
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
②过线段OA上的两点E、F分别作x轴的垂线,交折线O-B-A于E1、F1,再分别以线段EE1、FF1为边作如图2所示的等边△AE1E2、等边△AF1F2,点E以每秒1个长度单位的速度从点O向点A运动,点F以每秒1个长度单位的速度从点A向点O运动,当△AE1E2有一边与△AF1F2的某一边在同一直线上时,求时间t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).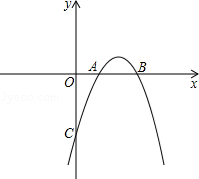
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0, ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知△ABC中,边BC的长与BC边上的高的和为20.
(1)写出△ABC的面积y与BC的长x之间的函数关系式,并求出面积为48时BC的长;
(2)当BC多长时,△ABC的面积最大?最大面积是多少?
(3)当△ABC面积最大时,是否存在其周长最小的情形?如果存在,请说出理由,并求出其最小周长;如果不存在,请给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:关于x的二次函数 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2,请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川攀枝花12分)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com