
【题目】已知数轴上有![]() 六个点,点
六个点,点![]() 在原点位置,点
在原点位置,点![]() 表示的数为
表示的数为![]() ,已知下表中
,已知下表中![]() 的含义均为前一个点所表示的数与后一个点所表示的数的差,比如
的含义均为前一个点所表示的数与后一个点所表示的数的差,比如![]() 为
为![]() .
.
|
|
|
|
|
|
|
|
|
|
若点![]() 与点
与点![]() 的距离为
的距离为![]() ,则
,则![]() 的值为________
的值为________
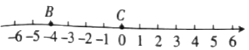
科目:初中数学 来源: 题型:
【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:![]() 如果正整数
如果正整数![]() 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外学习时间情况,随机抽取部分学生进行问卷调查,并将调查结果分为 A,B,C,D 四个等级.设学习时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2 ,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
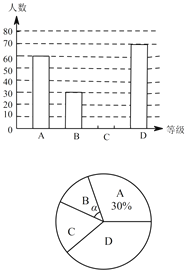
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示 B等级的扇形圆心角 α 的度数;
(4)在此次问卷调查中,甲班有 2 人平均每天课外学习时间超过 2 小时,乙班有 3 人平均每天课外学习时间超过 2 小时,若从这 5 人中任选 2人去参加座谈,试用列表或画树状图的方法求选出的2人
来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施乡村振兴战略,解决某山区老百娃出行难的问题,当地政府决定修建一条高速公路,其中一段长为146米的山体隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两个工程队又联合工作了1天,这3天共掘进26米,已知甲工程队平均每天比乙工程队多掘进2米.
(1)求甲、乙两个工程队平均每天分别掘进多少米?
(2)若甲、乙两个工程队按此施工速度进行隧道贯穿工程,剩余工程由这两个工程队联合施工,求完成这项隧道贯穿工程一共需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.
(1)求一个篮球和一个足球的售价各是多少元?
(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
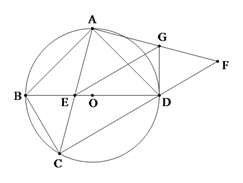
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
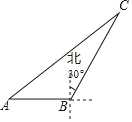
【题目】如图,海中一渔船在A处与小岛C相距70海里,若该渔船由西向东航行30海里到达B处,此时测得小岛C位于B的北偏东30°方向上,则该渔船此时与小岛C之间的距离是_____海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 的路线以
的路线以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
![]()
(1)当![]() 时,则线段
时,则线段![]()
![]() ,线段
,线段![]()
![]() .
.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 的中点为
的中点为![]() ,问
,问![]() 的长是否变化?与点
的长是否变化?与点![]() 的位置是否无关?
的位置是否无关?
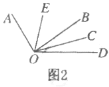
(4)知识迁移:如图2,已知![]() ,过角的内部任一点
,过角的内部任一点![]() 画射线
画射线![]() ,若
,若![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,问∠EOC的度数是否变化?与射线
,问∠EOC的度数是否变化?与射线![]() 的位置是否无关?
的位置是否无关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com