
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC
上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、MN、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
【小题1】DM=___▲____, AN=___▲____(用含x的代数式表示)
【小题2】说明△FMN  ∽ △QWP;
∽ △QWP;
【小题3】试问 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形? 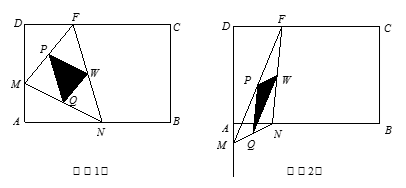
【小题4】问当 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?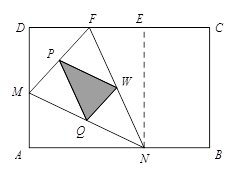
【小题1】
 ( 2分)
( 2分)
【小题2】∵P、Q、W分别为△FMN三边的中点
∴PQ∥FN,PW∥MN
∴∠MNF=∠PQM=∠QPW
同理:∠NFM=∠PQW
∴△FMN ∽ △QWP (2分)
【小题3】由⑴得△FMN ∽ △QWP,所以△FMN为直角三角形时,△QWP也为直角三角形.如图,过点N作NECD于E,根据题意,得DM=BM=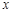 ,∴AM=4-
,∴AM=4-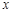 ,AN=DE=6-
,AN=DE=6-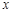
∵DF=2,∴EF=4-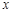
∴MF2=22+x2=x2+4,MN2=(4-x)2+(6-x)2=2x2-20x+52,
NF2=(4-x)2+42=x2-8x+32,
① 如果∠MNF=90°,
有2x2-20x+52+x2-8x+32=x2+4,
解得x1=4,x2=10(舍去);
②如果∠NMF=90°,
有2x2-20x+52+x2+4=x2-8x+32,
化简,得:x2-6x+12=0,△=-12<0, 方程无实数根;
③如果∠MFN=90°,
有2x2-20x+52=x2+4+x2-8x+32,
解得x=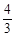 .
.
∴当 为4或
为4或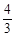 时,△PQW为直角三角形 (3分)
时,△PQW为直角三角形 (3分)
【小题4】当 =5时,线段MN最短.(2分)
=5时,线段MN最短.(2分)
解析


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
 根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.
根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com