
ЁОЬтФПЁПдФЖСвдЯТФкШнВЂЛиД№ЮЪЬтЃК
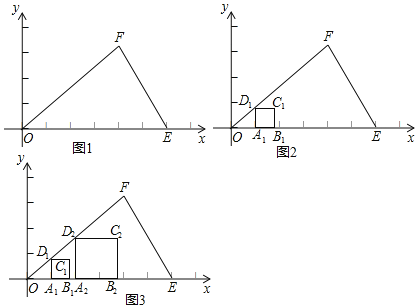
ШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌгавЛИіЁїOEFЃЌвЊЧѓдкЁїOEFФкзївЛИіФкНге§ЗНаЮABCDЃЌЪЙе§ЗНаЮAЃЌBСНИіЖЅЕудкЁїOEFЕФOEБпЩЯЃЌСэСНИіЖЅЕуCЃЌDЗжБ№дкEFКЭOFСНЬѕБпЩЯЃЎ
аЁРіИаЕНвЊЪЙЫФБпаЮЕФЫФИіЖЅЕуЭЌЪБТњзуЩЯЪіЬѕМўгааЉРЇФбЃЌЕЋПЩвдЯШШУЫФБпаЮЕФШ§ИіЖЅЕуТњзуЬѕМўЃЌгкЪЧЫ§ЯШЛСЫвЛИігаШ§ИіЖЅЕудкШ§НЧаЮБпЩЯЕФе§ЗНаЮЃЈШчЭМ2ЃЉЃЎНгзХЫ§гждкЁїOEFФкЛСЫвЛИіетбљЕФе§ЗНаЮЃЈШчЭМ3ЃЉЃЎЫ§ЗЂЯжШчЙћдйЖрЛвЛаЉетбљЕФе§ЗНаЮЃЌОЭФмЗЂЯжетаЉЕуCЮЛжУЕФХХСаЭМаЮЃЌИљОнетИіЭМаЮОЭФмЛГіТњзуЬѕМўЕФе§ЗНаЮСЫЃЎ
ЃЈ1ЃЉЧыФувВЪЕбщвЛЯТЃЌдйЖрЛМИИіетбљЕФе§ЗНаЮЃЌВТЯыаЁРіЗЂЯжетаЉЕуCХХСаЕФЭМаЮЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыФуВЮПМЩЯЪіЫМТЗЃЌМЬајНтОіЮЪЬтЃКШчЙћEЃЌFСНЕуЕФзјБъЗжБ№ЮЊEЃЈ6ЃЌ0ЃЉЃЌFЃЈ4ЃЌ3ЃЉЃЎ
ЂйЕБA1ЕФзјБъЪЧЃЈ1ЃЌ0ЃЉЪБЃЌдђC1ЕФзјБъЪЧЁЁ ЁЁЃЛ
ЂкЕБA2ЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЪБЃЌдђC2ЕФзјБъЪЧЁЁ ЁЁЃЛ
ЂлНсКЯЃЈ1ЃЉжаВТЯыЃЌЧѓГіе§ЗНаЮABCDЕФЖЅЕуDЕФзјБъЃЌдкЭМ3жаЛГіТњзуЬѕМўЕФе§ЗНаЮABCDЃЎ
ЁОД№АИЁПЃЈ1ЃЉвЛЬѕЯпЖЮЃЛЃЈ2ЃЉЂйЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЂкЃЈ
ЃЉЃЛЂкЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛDЕузјБъЮЊЃЈ
ЃЉЃЛDЕузјБъЮЊЃЈ![]() ЃЌ2ЃЉЃЌЂлМћНтЮі.
ЃЌ2ЃЉЃЌЂлМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§ЛЭМЃЌПЩжБНгЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШШЗЖЈГіжБЯпOFЕФНтЮіЪНЃЌ
ЂйНЋxЃН1ДњШыжБЯпOFНтЮіЪНЧѓГіyЃЌМДПЩЕУГіНсТлЃЛ
ЂкНЋxЃН2ДњШыжБЯпOFНтЮіЪНЧѓГіyЃЌМДПЩЕУГіНсТлЃЛ
ЂлЯШЧѓГіжБЯпC1C2ЕФБэДяЪНЮЊyЃН![]() xКЭжБЯпEFЕФБэДяЪНЮЊyЃНЉ
xКЭжБЯпEFЕФБэДяЪНЮЊyЃНЉ![]() +9ЃЌНјЖјЧѓГіCЕузјБъЮЊЃЈ
+9ЃЌНјЖјЧѓГіCЕузјБъЮЊЃЈ![]() ЃЌ2ЃЉЃЌМДПЩЕУГіНсТлЃЎ
ЃЌ2ЃЉЃЌМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЭЈЙ§ЛЭМЃЌВТЯыаЁРіЗЂЯжетаЉЕуCХХСаЕФЭМаЮЪЧвЛЬѕЯпЖЮЃЛ
ЙЪД№АИЮЊЃКвЛЬѕЯпЖЮЃЛ
ЃЈ2ЃЉЁпFЃЈ4ЃЌ3ЃЉЃЎ
ЁржБЯпOFЕФБэДяЪНЪЧyЃН![]() xЃЌ
xЃЌ
ЂйЁпЫФБпаЮA1B1C1D1ЪЧе§ЗНаЮЃЌ
ЁрA1D1ЃНA1B1ЃЌ
АбxЃН1ДњШыжБЯпyЃН![]() xжаЃЌЕУyЃН
xжаЃЌЕУyЃН![]() ЃЌ
ЃЌ
ЁрOB1ЃНOA1+A1B1ЃН1+![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрC1ЕФзјБъЪЧ ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЁпЫФБпаЮA2B2C2D2ЪЧе§ЗНаЮЃЌ
ЁрA2D2ЃНA2B2ЃЌ
АбxЃН2ДњШыжБЯпyЃН![]() xжаЃЌЕУyЃН
xжаЃЌЕУyЃН![]() ЃЌ
ЃЌ
ЁрOB2ЃНOA2+A2B2ЃН2+![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрC2ЕФзјБъЪЧ ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂлЩшЙ§C1ЃЌC2СНЕуЕФвЛДЮКЏЪ§БэДяЪНЪЧyЃНkx+bЃЈkЁй0ЃЉЃЎ
ДњШыC1ЃЌC2СНЕуЕУ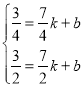 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпC1C2ЕФБэДяЪНЮЊyЃН![]() xЃЌ
xЃЌ
ЩшЙ§EЃЈ6ЃЌ0ЃЉЃЌFЃЈ4ЃЌ3ЃЉСНЕуЕФвЛДЮКЏЪ§БэДяЪНЪЧyЃНk'x+b'ЃЈk'Ёй0ЃЉЃЎ
ДњШыEЃЌFСНЕуЕУ![]()
НтЕУ ЃЌ
ЃЌ
ЫљвджБЯпEFЕФБэДяЪНЮЊyЃНЉ![]() x+9
x+9
жБЯпEFЃКyЃНЉ![]() x+9гыжБЯпC1C2ЃКyЃН
x+9гыжБЯпC1C2ЃКyЃН![]() xЕФНЛЕузјБъЮЊCЃЎ
xЕФНЛЕузјБъЮЊCЃЎ
СЊСЂжБЯпEFКЭжБЯпC1C2НтЮіЪНГЩЗНГЬзщВЂЧѓНтЕУЃКxЃН![]() ЃЌyЃН2ЃЎ
ЃЌyЃН2ЃЎ
ЁрCЕузјБъЮЊЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
АбyЃН2ДњШыyЃН![]() xЃЌНтЕУxЃН
xЃЌНтЕУxЃН![]() ЃЌ
ЃЌ
ЁрDЕузјБъЮЊЃЈ![]() ЃЌ2ЃЉ
ЃЌ2ЃЉ
ЫљЛЫФБпаЮABCDШчЭМ3ЫљЪОЃЌ



 ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИ
ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУГпЙцдквЛИіЦНааЫФБпаЮФкзїСтаЮ![]() ,ЯТСазїЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ
,ЯТСазїЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ

A. ЃЈAЃЉ B. ЃЈBЃЉ C. ЃЈCЃЉ D. ЃЈDЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
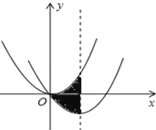
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=![]() x2ОЙ§ЦНвЦЕУЕНХзЮяЯпy=ax2+bxЃЌЦфЖдГЦжсгыСНЖЮХзЮяЯпЫљЮЇГЩЕФвѕгАВПЗжЕФУцЛ§ЮЊ
x2ОЙ§ЦНвЦЕУЕНХзЮяЯпy=ax2+bxЃЌЦфЖдГЦжсгыСНЖЮХзЮяЯпЫљЮЇГЩЕФвѕгАВПЗжЕФУцЛ§ЮЊ![]() ЃЌдђaЁЂbЕФжЕЗжБ№ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђaЁЂbЕФжЕЗжБ№ЮЊЃЈЁЁЁЁЃЉ
A. ![]() ЃЌ
ЃЌ![]() B.
B. ![]() ЃЌЉ
ЃЌЉ![]() C.
C. ![]() ЃЌЉ
ЃЌЉ![]() D. Љ
D. Љ![]() ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧжаЙњЙХДњЪ§бЇзЈжјЃЌдкЪ§бЇЩЯгаЦфЖРЕНЕФГЩОЭЃЌВЛНізюдчЬсЕНСЫЗжЪ§ЮЪЬтЃЌвВЪзЯШМЧТМСЫЁАгЏВЛзуЁБЕШЮЪЬт.ШчгавЛЕРВћЪіЁАгЏВЛзуЁБЕФЮЪЬтЃЌдЮФШчЯТЃКНёгаЙВТђМІЃЌШЫГіОХЃЌгЏЪЎвЛЃЛШЫГіСљЃЌВЛзуЪЎСљ.ЮЪШЫЪ§ЁЂМІМлИїМИКЮЃПвыЮФЮЊЃКЯжгаШєИЩШЫКЯЛяГіЧЎТђМІЃЌШчЙћУПШЫГі9ЮФЧЎЃЌОЭЛсЖр11ЮФЧЎЃЛШчЙћУПШЫГі6ЮФЧЎЃЌгжЛсШБ16ЮФЧЎ.ЮЪТђМІЕФШЫЪ§ЁЂМІЕФМлИёИїЪЧЖрЩйЃПЧыНтД№ЩЯЪіЮЪЬт.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃК
Ђй (Љ21)+(Љ13)Љ(Љ25)Љ(+28ЃЉ
Ђк Љ22Љ6ЁТЃЈЉ2ЃЉЁС![]()
ЂлЯШЛЏМђдйЧѓжЕЃКЉa2b+ЃЈ3ab2Љa2bЃЉЉ2ЃЈ2ab2Љa2bЃЉЃЌЦфжа a=Љ1ЃЌb=Љ2ЃЎ
ЃЈ2ЃЉНтЯТСаЗНГЬ
ЂйxЃН1Ѓ(3 xЃ1)
Ђк ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕШбќжБНЧШ§НЧаЮABCЕФбќГЄЮЊ2ЃЌжБНЧЖЅЕуAдкжБЯпlЃКy=2x+2ЩЯвЦЖЏЃЌЧваББпBCЁЮxжсЃЌЕБЁїABCдкжБЯпlЩЯвЦЖЏЪБЃЌBCЕФжаЕуDТњзуЕФКЏЪ§ЙиЯЕЪНЮЊЃЈ ЃЉ

A. y=2x B. y=2x+1 C. y=2x+2Љ![]() D. y=2xЉ
D. y=2xЉ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОдк![]() СНЕиЗжБ№ПтДцгаЭкОђЛњ16ЬЈКЭ12ЬЈЃЌЯждкдЫЭљМзЁЂввСНЕижЇдЎНЈЩшЃЌЦфжаМзЕиашвЊ15ЬЈЃЌввЕиашвЊ13ЬЈ.Дг
СНЕиЗжБ№ПтДцгаЭкОђЛњ16ЬЈКЭ12ЬЈЃЌЯждкдЫЭљМзЁЂввСНЕижЇдЎНЈЩшЃЌЦфжаМзЕиашвЊ15ЬЈЃЌввЕиашвЊ13ЬЈ.Дг![]() ЕидЫвЛЬЈЕНМзЁЂввСНЕиЕФЗбгУЗжБ№ЪЧ500дЊКЭ400дЊЃЛДг
ЕидЫвЛЬЈЕНМзЁЂввСНЕиЕФЗбгУЗжБ№ЪЧ500дЊКЭ400дЊЃЛДг![]() ЕидЫвЛЬЈЕНМзЁЂввСНЕиЗбгУЗжБ№ЪЧ300дЊКЭ600дЊЃЌЩшДг
ЕидЫвЛЬЈЕНМзЁЂввСНЕиЗбгУЗжБ№ЪЧ300дЊКЭ600дЊЃЌЩшДг![]() ЕидЫЭљМзЕи
ЕидЫЭљМзЕи![]() ЬЈЭкОђЛњЃЎ
ЬЈЭкОђЛњЃЎ
ЃЈ1ЃЉЧыВЙШЋЯТБэЃЌВЂЧѓГідЫетХњЭкОђЛњЕФзмЗбгУЪЧЖрЩйЃП
Мз | вв | змМЦ | |
|
| ____________ЬЈ | 16ЬЈ |
| _______________ЬЈ | ____________ЬЈ | 12ЬЈ |
змМЦ | 15ЬЈ | 13ЬЈ | 28ЬЈ |
ЃЈ2ЃЉЕБДг![]() ЕидЫЭљМзЕи5ЬЈЭкОђЛњЪБЃЌдЫетХњЭкОђЛњЕФзмЗбгУЪЧЖрЩйЃП
ЕидЫЭљМзЕи5ЬЈЭкОђЛњЪБЃЌдЫетХњЭкОђЛњЕФзмЗбгУЪЧЖрЩйЃП
ЃЈ3ЃЉдѕбљАВХХдЫЪфЗНАИЃЌПЩЪЙдЫетХњЭкОђЛњЕФзмЗбгУзюЩйЃЌзюЩйЗбгУЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
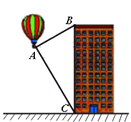
ЁОЬтФПЁПШШЦјЧђЕФЬНВтЦїЯдЪОЃЌДгШШЦјЧђAПДвЛЖАИпТЅЖЅВПBДІЕФбіНЧЮЊ30ЃЌПДетЖАИпТЅЕзВПCДІЕФИЉНЧЮЊ60ЃЌШєШШЦјЧђгыИпТЅЕФЫЎЦНОрРыЮЊ90 mЃЌдђетЖАИпТЅгаЖрИпЃПЃЈНсЙћБЃСєећЪ§ЃЌ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
ШєAЃЌBЃЌCЮЊЪ§жсЩЯШ§ЕуЧвЕуCдкAЃЌBжЎМфЃЌШєЕуCЕНAЕФОрРыЪЧЕуCЕНBЕФОрРыЕФ3БЖЃЌЮвУЧОЭГЦЕуCЪЧЃЈAЃЌBЃЉЕФКУЕуЃЎ

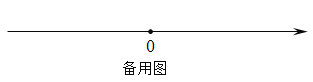
Р§ШчЃЌШчЭМ1ЃЌЕуAБэЪОЕФЪ§ЮЊЃ2ЃЌЕуBБэЪОЕФЪ§ЮЊ2ЃЎБэЪО1ЕФЕуCЕНAЕФОрРыЪЧ3ЃЌЕНBЕФОрРыЪЧ1ЃЌФЧУДЕуCЪЧЃЈAЃЌBЃЉЕФКУЕуЃЛгжШчЃЌБэЪОЃ1ЕФЕуDЕНAЕФОрРыЪЧ1ЃЌЕНBЕФОрРыЪЧ3ЃЌФЧУДЕуDОЭВЛЪЧЃЈAЃЌBЃЉЕФКУЕуЃЌЕЋЕуDЪЧЃЈBЃЌAЃЉЕФКУЕуЃЎ
жЊЪЖдЫгУЃК
ЃЈ1ЃЉШєMЁЂNЮЊЪ§жсЩЯСНЕуЃЌЕуMЫљБэЪОЕФЪ§ЮЊЃ6ЃЌЕуNЫљБэЪОЕФЪ§ЮЊ2ЃЎ
Ъ§ ЫљБэЪОЕФЕуЪЧЃЈMЃЌNЃЉЕФКУЕуЃЛ
Ъ§ ЫљБэЪОЕФЕуЪЧЃЈNЃЌMЃЉЕФКУЕуЃЛ
ЃЈ2ЃЉШєЕуAБэЪОЕФЪ§ЮЊaЃЌЕуBБэЪОЕФЪ§ЮЊbЃЌЕуBдкЕуAЕФгвБпЃЌЧвЕуBдкAЃЌ CжЎМфЃЌЕуBЪЧЃЈCЃЌAЃЉЕФКУЕуЃЌЧѓЕуCЫљБэЪОЕФЪ§ЃЈгУКЌaЁЂbЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉШєAЁЂBЮЊЪ§жсЩЯСНЕуЃЌЕуAЫљБэЪОЕФЪ§ЮЊЃ33ЃЌЕуBЫљБэЪОЕФЪ§ЮЊ27ЃЌЯжгавЛжЛЕчзгТьвЯPДгЕуAГіЗЂЃЌвдУПУы6ИіЕЅЮЛЕФЫйЖШЯђгвдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЎШчЙћPЃЌAЃЌBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com