Question

如图所示，已知△ACM和△CBN都是等边三角形，点A、C、B在同一直线上，连接AN、MB．

（1）求证：AN=BM．

（2）若等边三角形CBN绕顶点C顺时针旋转后（旋转角），此时AN与BM是否还相等?若相等，给出证明；若不相等，说明理由．

Answer 1

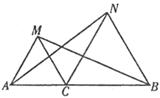
（1）

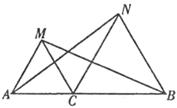
证明：在三角形ACM和NCB中，

因为，△ACM和△CBN是等边三角形，

所以，AC=MC，CB=CN．

∠ACM=∠NCB=60°，∠MCN=60°，

∠ACN=∠MCB=120°．

所以△ACN≌△MCB．

所以，AN=BM．

（2）AN与BM相等．

旋转角为，

当时，如下图

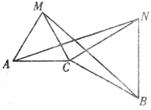
因为，△ACM和△CBN是等边三角形，

所以，AC=MC，CB=CN．

∠ACN=60°+∠MCN

∠MCB=60°+∠MCN

∠ACN=∠MCB．

所以，△ACN≌△MCB．

所以，AN=BM．

当时，A、C、N三点共线，M、C、B三点共线，

AN=AC+CN，BM=MC+CB=AC+CN

所以，AN=BM．

当时，如下图，

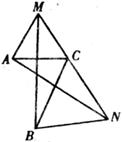
因为，△ACM和△CBN是等边三角形，

所以，AC=MC，CB=CN．

∠ACN=60°+∠ACB．

∠MCB=60°+∠ACB

∠ACN=∠MCB．

∴△ACN≌△MCB

∴AN=BM．