
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边的延长线上,且
边的延长线上,且![]() .
.
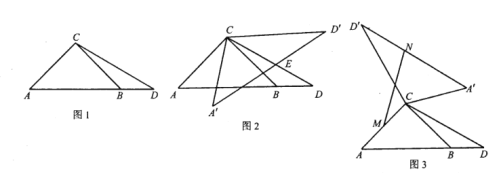
(1)求![]() 的度数;
的度数;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )得到
)得到![]() .
.
①若![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的长度;
的长度;
②连接![]() ,
,![]() ,若旋转过程中
,若旋转过程中![]() 时,求满足条件的
时,求满足条件的![]() 的度数.
的度数.
(3)如图3,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )得到
)得到![]() ,若点
,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点,直接写出旋转过程中,线段
上任意一点,直接写出旋转过程中,线段![]() 长度的取值范围为______.
长度的取值范围为______.
【答案】(1)∠ADC=30°;(2)①DE=![]() ;②45°或225°;(3)
;②45°或225°;(3)![]() .
.
【解析】
(1)过点C作CH⊥AB于H,由等腰直角三角形的性质和已知条件可得CH=![]() AB=
AB=![]() CD,再由锐角三角函数可求解;
CD,再由锐角三角函数可求解;
(2)①由旋转的性质和(1)题的结果可得![]() 的长,∠
的长,∠![]() =∠
=∠![]() ,由等腰三角形的性质和30°角的余弦可得CF与CE,进一步即可求出结果;
,由等腰三角形的性质和30°角的余弦可得CF与CE,进一步即可求出结果;
②分两种情况分别画出图形,如图3、图4,由旋转的性质可由“SSS”证明△![]() ≌△
≌△![]() ,可得∠
,可得∠![]() =∠
=∠![]() ,进而可得α的方程,解方程即得结果;
,进而可得α的方程,解方程即得结果;
(3)如图5,当![]() ⊥AC时,N是AC与
⊥AC时,N是AC与![]() 的交点时,MN的长度最小,如图6,当点A,C,
的交点时,MN的长度最小,如图6,当点A,C,![]() 共线,且点N与点
共线,且点N与点![]() 重合时,MN有最大值,进而可求结果.
重合时,MN有最大值,进而可求结果.
解:(1)如图1,过点C作CH⊥AB于H,

∵∠ACB=90°,AC=BC=6,CH⊥AB,
∴AB=6![]() ,CH=
,CH=![]() AB=3
AB=3![]() ,∠CAB=∠CBA=45°,
,∠CAB=∠CBA=45°,
∵AB=CD,
∴CH=![]() CD,
CD,
∴sin∠ADC=![]() ,
,
∴∠ADC=30°;
(2)①如图2,过点E作EF⊥![]() 于F,
于F,
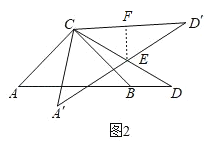
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△![]() ,
,
∴CD=![]() =6
=6![]() ,∠
,∠![]() =30°=∠CDA=∠
=30°=∠CDA=∠![]() ,
,
∴CE=![]() ,
,
又∵EF⊥![]() ,
,
∴CF=![]() =3
=3![]() ,
,
∴CE=![]() ,
,
∴DE=DC﹣CE=![]() ;
;
②如图3,

∵∠ABC=45°,∠ADC=30°,
∴∠BCD=15°,
∴∠ACD=105°,
∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△![]() ,
,
∴AC=![]() ,CD=
,CD=![]() ,∠
,∠![]() =∠
=∠![]() =α,
=α,
∴CB=![]() ,
,
又∵![]() ,
,
∴△![]() ≌△
≌△![]() (SSS),
(SSS),
∴∠![]() =∠
=∠![]() ,
,
∴105°﹣α=15°+α,
∴α=45°;
如图4,

同上面的方法可证:△![]() ≌△
≌△![]() ,
,
∴∠![]() =∠
=∠![]() ,
,
∴α﹣105°=360°﹣α﹣15°,
∴α=225°;
综上所述:满足条件的α的度数为45°或225°;
(3)如图5,当![]() ⊥AC,N是AC与
⊥AC,N是AC与![]() 的交点时,MN的长度最小,
的交点时,MN的长度最小,

∵∠![]() =45°,
=45°,![]() ⊥AC,
⊥AC,
∴∠![]() =∠
=∠![]() =45°,
=45°,
∴CN=![]() N=3
N=3![]() ,
,
∵点M为AC的中点,
∴CM=![]() AC=3,
AC=3,
∴MN的最小值=NC﹣CM=3![]() ﹣3;
﹣3;
如图6,当点A,C,![]() 共线,且点N与点
共线,且点N与点![]() 重合时,MN有最大值,
重合时,MN有最大值,

此时MN=CM+CN=6![]() +3,
+3,
∴线段MN的取值范围是![]() ;
;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为_____.
的图象上,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
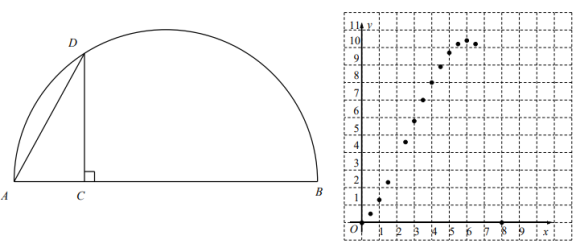
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的盒子中,分别装有除颜色外其它均相同的小球,其中,甲盒子装有2个白球,1个红球:乙盒子装有2个红球,1个白球.
(1)将甲盒子摇匀后,随机取出一个小球是红球的概率是______;
(2)小华和小明商定:将两个盒子摇匀后,各随机摸出一个小球.若颜色相同,则小华获胜;若颜色不同,则小明获胜,请用列表法或画出树状图的方法说明谁贏的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)小明认为口袋中共有三种颜色的球,所以从袋中任意摸出一球,摸到红球、白球或黄球的概率都是![]() ,你认为对吗?请你用列表或画树状图的方法说明理由.
,你认为对吗?请你用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
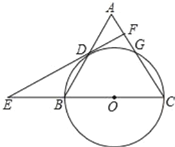
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为一幢高3米的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方的点A处建一幢高12米的楼房AB.(设A,C,F在同一水平线上)
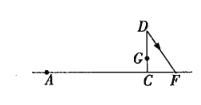
(1)作出楼房AB及它的最大影长AE;
(2)楼房AB建成后,其是否影响温室CD的采光?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com