
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)按照变量的定义,根据题意点P为动点,BE的长随着点P的移动而改变,BC为已知等腰直角三角形![]() 的斜边;
的斜边;
(2)描点画出图象即可;
(3)根据图形可求出![]() 长度根据
长度根据![]() 长度变化的函数关系式为一次函数,发现斜率绝对值接近
长度变化的函数关系式为一次函数,发现斜率绝对值接近![]() ,再通过画图可证明三条线段关系.
,再通过画图可证明三条线段关系.
(1)根据题意,画出图形,再结合表格数据可知,![]() 的长度是自变量,
的长度是自变量,![]() 的长度是这个自变量的函数,
的长度是这个自变量的函数,![]() 的长度是常量.
的长度是常量.
故答案为:![]() ,
,![]() ,
,![]() .
.
(2)根据表格数据描点画出以下图像
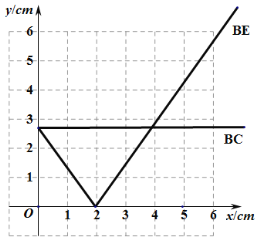
(3)首先通过函数图像图像,可判断BE关于BP的函数图像氛围两部分,斜率接近![]() ,则可知线段
,则可知线段![]() ,
,![]() ,
,![]() 之间的数量关系
之间的数量关系![]() .
.
再通过画图证明:
当点P在线段BA的延长线上时,如图,过点P作PF垂直于AC交BC的延长线于F,

∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() (
(![]() ),
),
∴![]() ,
,
在等腰直角三角形![]() 中,
中,![]()
∴![]() ,
,
即,![]() ;
;
当点P在线段AB上时,过点P作![]() 于点
于点![]() ,
,

同理可证![]() (
(![]() ),
),
∴![]() ,
,
∴![]() ,
,
又∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]()
综上:线段![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,BC=![]() AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
(1)判断四边形ABCE的形状,并说明理由;
(2)如果AB=4,∠D=30°,点P为BE上的动点,求△PAF的周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
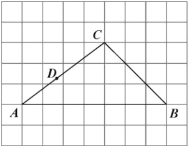
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
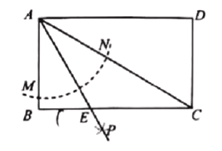
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c的图象如图所示,以下结论:①b
+bx+c的图象如图所示,以下结论:①b![]() >4ac;②b+2a<0;③当x<-
>4ac;②b+2a<0;③当x<-![]() ,y随x的增大而增大;④a-b+c<0中,正确的有( )
,y随x的增大而增大;④a-b+c<0中,正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE连接BE

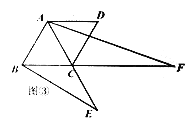
(1)发现问题:如图①,若E是线段AC的中点,连接EF,其他条件不变,猜想线段BE与EF的数量关系
(2)探究问题:如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想
(3)解决问题:如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=3请直接写出AF的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
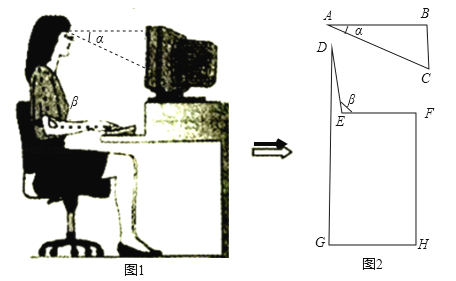
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
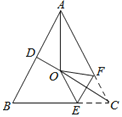
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com